CS 202 - Notes 2018-11-12
Combinational circuits
There are two types of circuits: circuits with memory and circuits without memory. Right now we are interested in the later, what we call combinational circuits, so called because their outputs are purely a function of the current combination of inputs.
To help us reason about combinational circuits, we use Boolean algebra, which provides us with our basic building blocks: AND, OR and NOT.
| A | B | A' (NOT A) | AB (A AND B) | A+B (A OR B) |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
We can express our functions in Boolean algebra, and then we can implement them using gates. In addition to AND, OR and NOT, we have NAND (NOT AND), NOR (NOT OR), XOR (exclusive OR) and XNOR (exclusive NOR) in our collection of available gates.
In addition to being able to express functions as Boolean expressions and as circuits, we can also express them as truth tables (seen above), where every possible combination of values of our input variables is paired with the corresponding output of the function. A proper truth table orders the rows as if we were counting in binary. This provides us with a canonical form so we can compare two truth tables, and makes it easier to find missing or duplicated rows.
Example: circuit to truth table
If we are trying to figure out what a circuit does, we can "simulate" it by trying all possible inputs and recording them in a truth table. To make it easier to keep track of, we will typically identify sub-circuits and look at their behavior (a,b,c in the diagram).
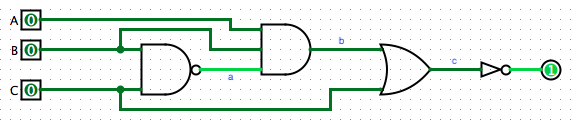
| A | B | C | a | b | c | Out |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 |
Example: Truth table to Boolean expression
There are several ways to write a Boolean expression from a truth table. One common way is to express the function as a sum of products.
We start by extracting the minterms from the table. The minterms are expressions that are true when one particular set of values indicate that the function is true. For example, the first row of the table tells us that the function is true when A, B and C are all false. So, the first minterm is A'B'C' (this term is true when A is false and B is false and C is false). Extracting all minterms gets us (A'B'C', A'BC', and AB'C').
We get the sum of products by ORing the minterms together (i.e., the function is true if any of the minterms are true): A'B'C' + A'BC' + AB'C'
Example: Simplification
as I said in class, I won't hold you responsible for anything other than the simplest forms of simplification. However, I will provide an example of what it looks like:
|A'B'C' + A'BC' + AB'C'|sum of products| |C'(A'B' + A'B + AB')|factoring out C'| |C'(A'B' + A'B + AB' + A'B')|X + X = X; duplicating A'B'| |C'(A'(B' + B) + AB' + A'B')|factoring out A'| |C'(A'(1) + AB' + A'B')|X + X' = 1| |C'(A' + AB' + A'B')|X(1) = X| |C'(A' + B'(A + A'))|factoring out B'| |C'(A' + B'(1))|X + X' = 1| |C'(A' + B')|X(1) = X|
Simplified form is `C'(A' + B').
Example: Word problem to circuit
Question: Should you work on your 202 homework?
We establish some variables:
- It is due tomorrow (D)
- There is currently time to work on it (T)
- This is a group project (G)
- My group project partner is free to work on it (P)
We can then encode the permutations of these variables as a truth table.
| Due | Time | Group | Partner | Work |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Extract the miterms and write out the sum of products
D'TG'P' + D'TG'P + D'TGP + DTG'P' + DTG'P + DTGP' + DTGP
Given a sum of products expression we can always create a circuit of the following form, with AND gates for the minterms and an OR gate tying them together.
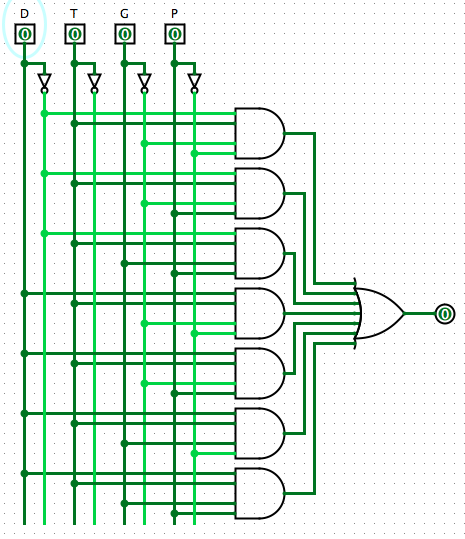
As a side note, in class I demonstrated that this could be simplified down to T(D + G' + GP). This makes sense as we can read this as "I have time and the work is due tomorrow or it isn't a group project, or it is a group project and my partner also has time".