Quantum Cryptography
1 Learning Goals
- Predict outcome of simple quantum polarization measurements
- Describe classical secret key protocol
- Understand key terms: encode/encrypt, decode/decrypte, secret key, encoded message
- Describe BB84 quantum cryptography protocol and why it is secure
2 Classical Secret Key Protocol and Intro to Quantum Cryptography
The characters:
- Alice: has a secret message \(m\in\{0,1\}^n\) that she wants to sent to Bob (and no one else)
- Bob: wants to receive the message from Alice
- Eve: can hear everything that Alice tries to send to Bob, and they know Alice and Bob’s plan for communication, but no secret information our results of private random coin flips.
If Alice and Bob have a secret key \(s\in \{0,1\}^n\) that they each know, but Eve does not know, they can securely communicate. (On your first problem set, you will look into why they can securely communicate.)
Problem: How to share the secret key?!
Current solution: Public Key Cryptography
Looming problem: Eve with a quantum computer can break public key cryptography and learn Alice’s message
Luckily, when one door closes (public key cryptography) another door opens (quantum cryptography). Quantum cryptography is a way for Alice and Bob to share a secret ket without being physically together.
To do quantum cryptography, we need qubits. There are many types of qubits, but for cryptography, it makes sense to use photons - individual particles of light. Photons are:
- Fast (good!)
- Easily lost in fiber-optic cables, in atmosphere (bad!)
- Hard to create and detect (bad!)
3 Photons and Polarizers
Notation: We describe photons and filters as “vertically/diagonally/horizontally polarized”
If I insert a diagonal polarized filter (diagonal polarizer) between a horizontal and vertically polarized filter, how much light will come through?
- Same as with no diagonal filter inserted
- Less than with a single filter
- The same as with a single filter
- More than with a single filter
A photon’s polarization is aligned with the filter
- The photon exits the filter unchanged
A photon’s polarization is perpendicular to the polarization of the filter
- The photon is blocked by the filter
A photon’s polarization is at a \(45^\circ\) angle to the filter
- With 1/2 probability, the photon exits with polarization the same as the filter
- With 1/2 probability, no photon exits
If you’ve never studied quantum before, your intuition for the final scenario was probably wrong! We think of the filter as forcing the photon to “choose” to be aligned or anti-aligned. To make the “decision,” the photon flips a coin (50/50 probability for the case of a \(45^\circ\) angle) and “collapses” to be in either an aligned or perpendicular state.
Ice breaker: how do you react in group problem solving scenarios? (e.g. I like to sit back and listen to others, I feel comfortable sharing my opinion, I like to lead the direction of the conversation, I feel uncomfortable in silences, I need time to think on my own before participating, I get frustrated when others don’t understand what I’m trying to say …)
Main question: Explain our experiment using your new understanding of photons and polarizers:
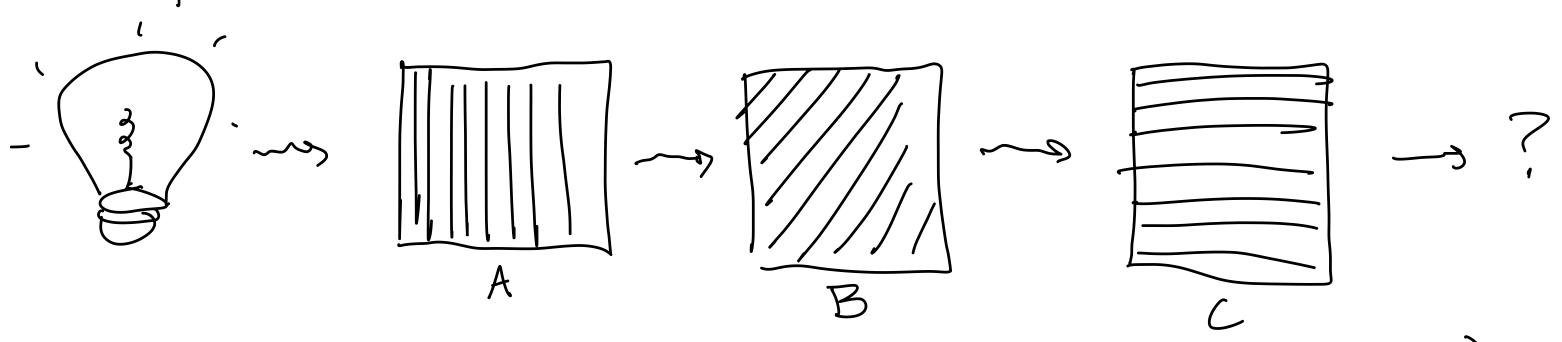
You should assume that each photon out of the bulb has a random polarization.
- What polarizations(s) do exiting photons have?
- If \(T\) photons hit polarizer \(B\), on average how many photons will exit polarizer C?
4 BB84 Quantum Cryptography Protocol
- Alice and Bob pick \(L\gg n\) (where recall \(n\) is the length of the message she wants to send.)
- Alice chooses \(a,b\in\{0,1\}^L\) randomly. At the \(i^{th}\) time step she sends a photon to Bob. The polarization of the photon is chosen based on \(a_i\), \(b_i\), (\(i^{th}\) bits of \(a\) and \(b\)) using the following table:
| \(a\) (basis bit) | \(b\) (info bit) | photon polarization | ket |
|---|---|---|---|
| 0 | 0 | vertical | \(\ket{0}\) |
| 0 | 1 | horizontal | \(\ket{1}\) |
| 1 | 0 | right diagonal | \(\ket{+}=\frac{1}{\sqrt{2}}\ket{0}+\frac{1}{\sqrt{2}}\ket{1}\) |
| 1 | 1 | left diagonal | \(\ket{-}=\frac{1}{\sqrt{2}}\ket{0}-\frac{1}{\sqrt{2}}\ket{1}\) |
- Bob chooses \(c\in\{0,1\}^L\) randomly. At the \(i^{th}\) time step he sets up a measurement based on \(c_i\) using the following table:
| \(c\) (measurement basis) | measurement | ket |
|---|---|---|
| 0 | vertical polarizer followed by photon detector | \(\{\ket{0},\ket{1}\}\) |
| 1 | right diagonal polarizer followed by photon detector | \(\{\ket{+},\ket{-}\}\) |
- Bob records the outcome of his measurement in the string \(d\), as:
\[ d_i= \begin{cases} 0 & \textrm{ if detection}\\ 1 & \textrm{ if no detection} \end{cases} \]
\(L=2\), \(a=01\), \(b=11\), \(c=11\).
Then Alice first sends a horizontally polarized photon to Bob, who measures it with a right diagonal filter. In this scenario, there is a 50/50 chance of detection, so \(d_1\) will either be \(0\) or \(1\) with equal probability.
Then Alice sends a left diagonally polarized photon to Bob, who measures it with a right diagonal filter. In this scenario, there is a 0 chance of detection, so \(d_2=1\).
Thus, in this example, Bob will either have \(d=01\) or \(d=11.\)
If \(a_i=c_i\) then
- \(b_i=d_i\)
- \(b_i\neq d_i\)
- \(b_i=d_i\) half of the time
If \(a_i\neq c_i\) then
- \(b_i=d_i\)
- \(b_i\neq d_i\)
- \(b_i=d_i\) half of the time
Alice and Bob publicly announce \(a\) and \(c\) strings.
Alice and Bob throw out the bits of \(b,d\) corresponding to bits where \(a\neq c\). The remaining bits (\(b'\) for Alice, \(d'\) for Bob) should be their secret key. (We should have \(b'=d'\).)
Here is a one-sheet description of Alice and Bob’s part of the protocol.
4.1 What about Eve??!!
Here is a possible strategy for Eve. They choose \(e\in\{0,1,2\}^L\) in the most malicious way possible. At the \(i^{th}\) time step they set up a measurement based on \(e_i\) using the following table:
| \(e\) | measurement | |
|---|---|---|
| 0 | vertical polarizer followed by photon detector | |
| 1 | right diagonal polarizer followed by photon detector | |
| 2 | lets the photon pass undisturbed |
If \(e_i\in\{0,1\}\):
- If they get a detection, they send to Bob a photon with the polarization of their polarizing filter. (For example, if they are measuring with a vertical polarizer and get a detection, they send a vertically polarized photon to Bob.)
- If they do not get a detection, they send to Bob a photon with a polarization 90 degrees away from that of their filter. (For example, if they are measuring with a vertical polarizer and do not get a detection, they send a horizontally polarized photon to Bob.)
Eve records their outcome in the string \(f:\) \[ f_i= \begin{cases} 0 & \textrm{ if detection}\\ 1 & \textrm{ if measure but no detection} \\ 2 & \textrm{ if no measurement} \end{cases} \]
To help visualize this scenario and play around with Alice’s, Bob’s, and Eve’s choices, can check out this applet by St. Andrews University
4.2 Group Exercise
[QI5 warmup]
Ice breaker: What clubs/sports/activities do you participate in at Midd?
- Suppose at some round Alice has chosen \(a=0\), \(b=0\) and Bob has chosen \(c=0\), so Alice prepares a vertically polarized photon, and Bob measures in the vertical/horizontal basis. Now suppose Eve inserts herself between Alice and Bob and possibly measures the photon. For each of Eve’s possible choices for \(e\), (\(0,1\) or \(2\)), what values will \(d\) and \(f\) take, with what probabilities?
- What does Eve learn about the secret key?
- How does Eve’s action affect the key?
- What about other scenarios where \(a=c\)?
- Why can we ignore cases when \(a\neq c\)?
We see that the more Eve interferes (chooses \(e_i\) to be \(0\) or \(1\)), the more \(b'\neq d'\). This seems bad, because Alice and Bob’s shared secret key should be the same. And also, now Eve knows information about \(b'\) and \(d'\), even though these should be secret. This seems bad!! How do we make this ok?
To deal with Eve’s interference or possible interference, Alice and Bob need to add a few more steps to their protocol:
Alice and Bob make public a random subset of the bits of \(b'\) and \(d'\). If Eve did not interfere, these should all be the same. If they interfered a lot, \(b'\) and \(d'\) will be somewhat different. By counting how many of these public bits are the same, they can estimate how often Eve interfered, and consequently, they can estimate how much information Eve knows about the rest (the as yet unpublicized bits) of \(b'\) and \(d'\) (which we call \(b''\), \(d''\)). Now if there are a lot of mismatches, Alice and Bob decide that Eve knows too much, and they abort the protocol. This is the equivalent of Eve jamming their signal. However, if there are not too many mismatches, they conclude Eve does not know very much about their remaining bits, and they decide to continue.
Alice and Bob perform an error correction protocol on \(b''\) and \(d''\) to end up with an identical string \(s'\) that they each possess. (The details of this protocol are beyond the scope of this class.) The important things to know about this error correction protocol are:
- \(|s'|<|b'|,|d'|\) (they lose bits in the process)
- Eve learns some additional information about \(s'\) in this process because they know what error correction protocol Alice and Bob are using, but they do not learn too much information
- Alice and Bob perform privacy amplification. They do this by applying a hash function to \(s'\) to produce a string \(s\). The important things to know:
- \(|s|<|s'|\) (they lose bits of their secret key in the process)
- Eve knows nothing about \(s\), even though they had some information about \(s'\) and know the hashing function used.
[QI5 warmup]
Ice breaker: Song of the summer?
- Talk through the BB84 protocol. Try to explain each part, what is going on, and why.
- Create a list of questions that you can not answer as a group
- BB84 creates a secret key that is guaranteed secure from any eavesdropper. What is the quantum secret sauce that allows this?