Bomb Detection
\[ \newcommand{\braket}[2]{\langle{#1}|{#2}\rangle} \]
1 Learning Goals
- Describe quantum operations
- Describe partial quantum measurements
- Use rules of quantum operations and partial quantum measurements to analyze abstract and interferometer scenarios
2 Bomb Detection (Elitzur-Vaidman Bomb Tester)
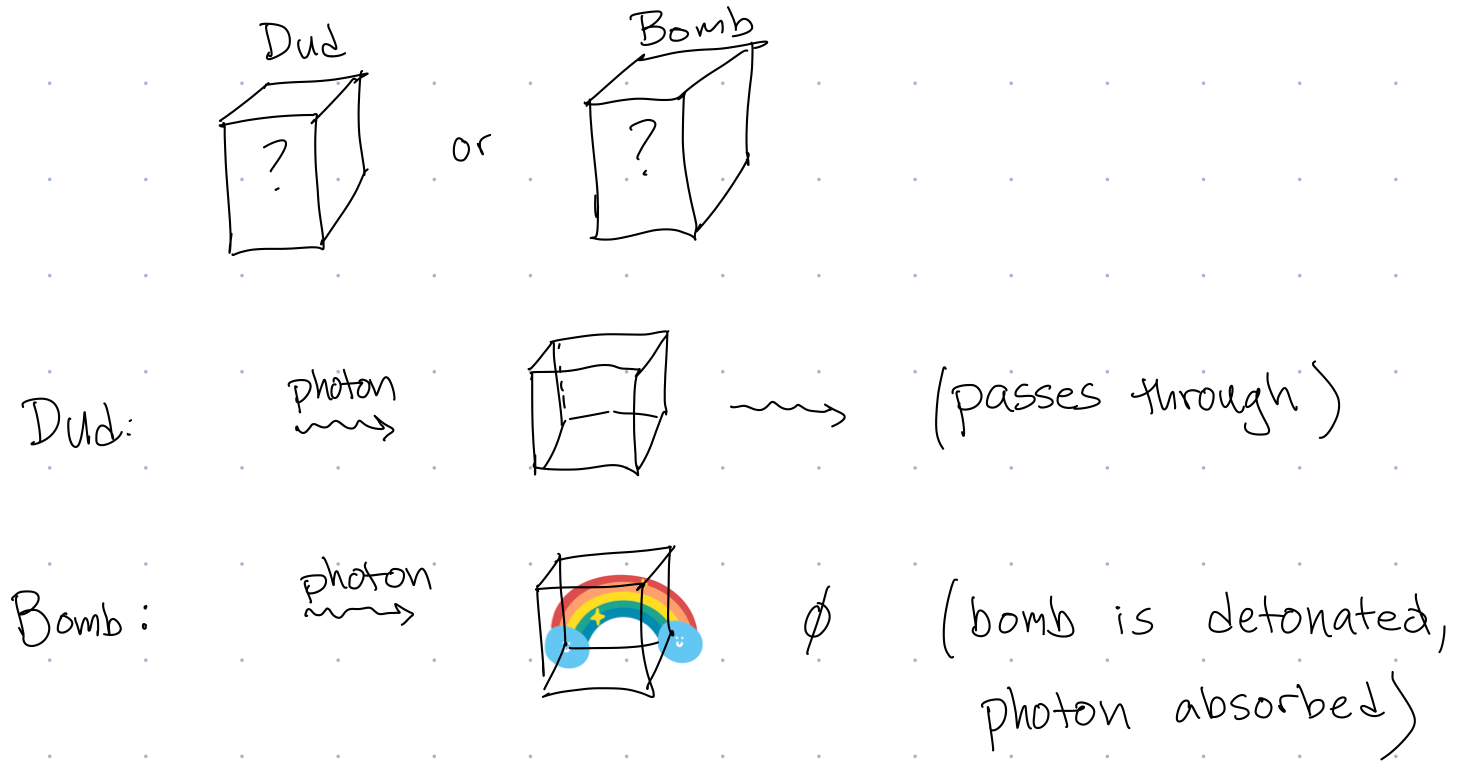
For this problem, we imagine we have devices called rainbow bombs. These bombs look like clear boxes. But if you shoot a single photon into a rainbow bomb, the photon will trigger the bomb, which will absorb the photon and explode into a rainbow. Once a bomb explodes, it can not be used again. The problem is that the manufacturing process is inconsistent, and sometimes it produces a dud. The duds look exactly the same as a bomb (a clear box) except now, if you shoot a photon at a dud, the photon will pass right through the box unaffected.
Someone has given you a potential rainbow bomb, and you would like to determine if it is a live bomb or a dud…without detonating it. The figure below lays out the situation in pictures:
3 Beamsplitters, Gates, Interferometers, and Partial Measurements
3.1 Beamsplitters
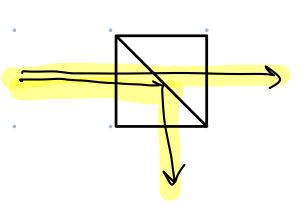
To detect a bomb without detonating it, we will need a new type of quantum tool called a gate. The first gate we will look at is called a beamsplitter, and is represented graphically as a box with a diagonal like through it:

The beamsplitter either transmits light or reflects light depending on the polarization of the incoming photon. If the photon is vertically polarized, the beamsplitter transmits the photon. If the photon is horizontally polarized, the beamsplitter reflects the photon at at \(90^\circ\) angle.
When we send a single photon into a beamsplitter, we need two qubits to describe the system. One qubit is used to describe the polarization of the photon. (We use a subscript \(P\) to represent this qubit.) One qubit is used to describe the direction the photon is traveling in. (We use a subscript \(D\) to represent this qubit.) The standard basis states of the direction qubit are \(\ket{V}_D\), which is when the photon is traveling vertically, and \(\ket{H}_D\), which is when the photon is traveling horizontally. The direction qubit can describe the state of the qubit either before or after it encounters the beamsplitter:
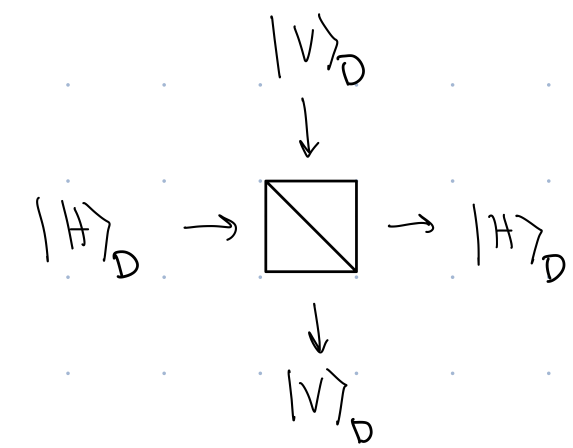
Behavior of the beamsplitter:
If we have a vertically polarized photon traveling in the horizontal direction to the right into the beamsplitter, it does not get reflected and travels straight through the beamsplitter, continuing in the horizontal direction, still with vertical polarization. We can write this transformation with kets as \[\ket{0}_P\ket{H}_D\rightarrow\ket{0}_P\ket{H}_D \]
If we have a horizontally polarized photon traveling in the horizontal direction into the beamsplitter, it gets reflected and exits the beamsplitter downwards in the vertical direction still with vertically polarized light. We can write this transformation with kets as \[\ket{1}_P\ket{H}_D\rightarrow\ket{1}_P\ket{V}_D \]
- If we have a vertically polarized photon traveling vertically downwards into the beamsplitter, what transformation occurs? \[\ket{0}_P\ket{V}_D\rightarrow ?\]
- \(\ket{0}_P\ket{H}_D\)
- \(\ket{0}_P\ket{V}_D\)
- \(\ket{1}_P\ket{H}_D\)
- \(\ket{1}_P\ket{V}_D\)
- If we have a horizontally polarized photon traveling vertically downwards into the beamsplitter, what transformation occurs? \[\ket{1}_P\ket{V}_D\rightarrow ?\]
- \(\ket{0}_P\ket{H}_D\)
- \(\ket{0}_P\ket{V}_D\)
- \(\ket{1}_P\ket{H}_D\)
- \(\ket{1}_P\ket{V}_D\)
3.2 Quantum Gates
A gate is an operation that changes a quantum state without causing a collapse. We can describe the action of the gate based on how it transforms standard basis states:
Beamsplitter \[ \begin{align} \ket{0}_P\ket{H}_D&\rightarrow\ket{0}_P\ket{H}_D\\ \ket{0}_P\ket{V}_D&\rightarrow\ket{0}_P\ket{V}_D\\ \ket{1}_P\ket{H}_D&\rightarrow\ket{1}_P\ket{V}_D\\ \ket{1}_P\ket{V}_D&\rightarrow\ket{1}_P\ket{H}_D \end{align} \]
\(45^\circ\) Mirror \[ \begin{align} \ket{H}_D&\rightarrow\ket{V}_D\\ \ket{V}_D&\rightarrow\ket{H}_D \end{align} \]
\(45^\circ\) Waveplate \[ \begin{align} \ket{0}_P&\rightarrow\ket{+}_P\\ \ket{1}_P&\rightarrow\ket{-}_P \end{align} \]
\(90^\circ\) Waveplate \[ \begin{align} \ket{0}_P&\rightarrow\ket{1}_P\\ \ket{1}_P&\rightarrow\ket{0}_P \end{align} \]
These gates are represented graphically as 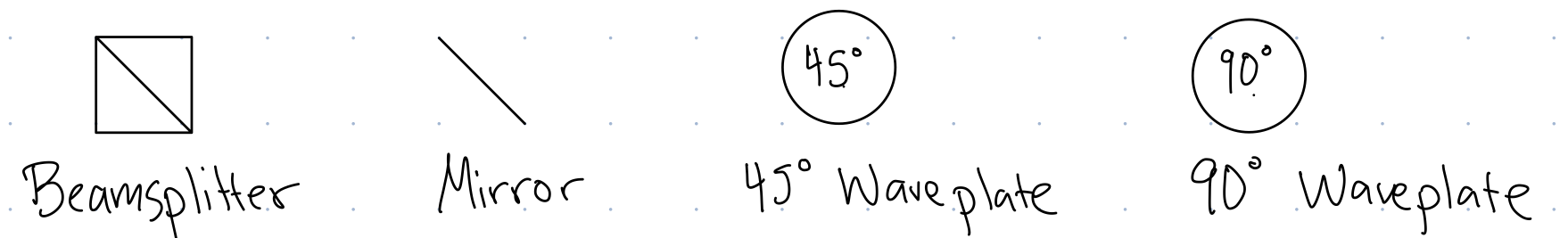
3.3 Interferometer
[QI4]
Now we can combine all of these gates into a device called an interferometer:
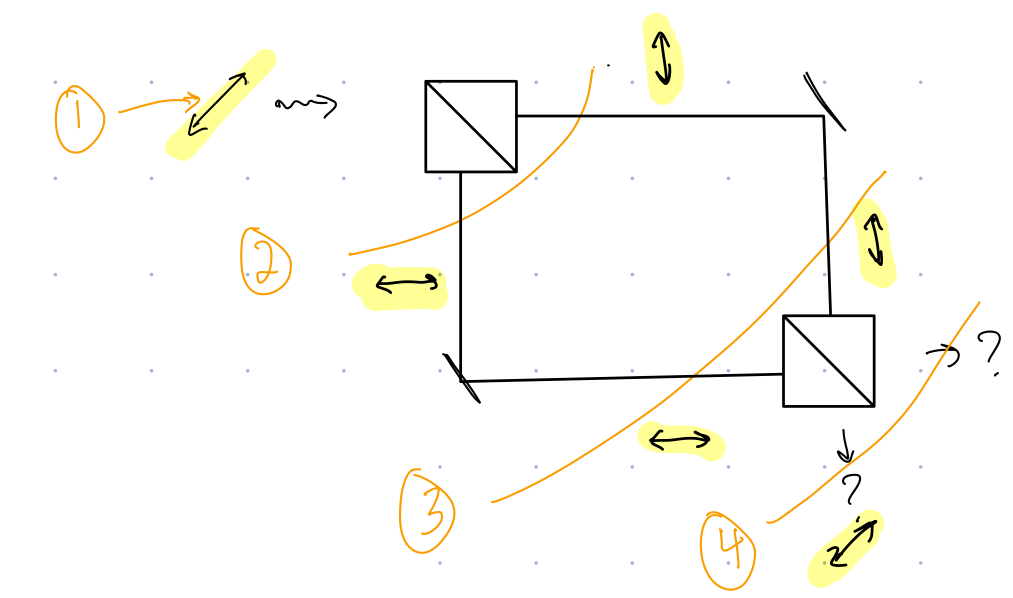
To analyze this system, we will study how the quantum state changes as it goes through the interferometer. We call \(\ket{\psi_1}\) the initial state of the system (labeled by \(1\) in the picture), then \(\ket{\psi_2}\) will label the state of the system after the photon passes through the first beamsplitter, etc.
We start with the initial state of the system, which is a right diagonally polarized photon traveling to the right:
\[\ket{\psi_1}=\ket{+}_P\ket{H}_D\]
Next the beamsplitter acts on \(\ket{\psi_1}\). Gates act on kets left to right. I’ll use the \(\square\) symbol on this document to represent the beamsplitter: \[\ket{\psi}=\square\ket{+}_P\ket{H}_D\]
Now we have a problem, because we only know how the beamsplitter transforms standard basis states, not the state \(\ket{+}\). But because any state can be written as a linear combination of standard basis states, this is OK! So we next write \(\ket{+}\) using standard basis states: \[ \begin{align} \ket{\psi_2}=&\square\left(\frac{1}{\sqrt{2}}\ket{0}_P+\frac{1}{\sqrt{2}}\ket{1}_P\right)\ket{H}_D\\ =&\square\frac{1}{\sqrt{2}}\ket{0}_P\ket{H}_D+\square\frac{1}{\sqrt{2}}\ket{1}_P\ket{H}_D \end{align}\] where in the second line we have distributed the \(\square\) and \(\ket{H}_D\) terms, being sure to maintain the order of gates and kets.
Now while the order of gates and kets should state the same (they don’t commute), scalars (numbers) do commute with everything, so we can move the \(\frac{1}{\sqrt{2}}\) before the beamsplitter symbols to get: \[ \begin{align} \ket{\psi_2} =&\frac{1}{\sqrt{2}}\square\ket{0}_P\ket{H}_D+\frac{1}{\sqrt{2}}\square\ket{1}_P\ket{H}_D \end{align}\]
Finally, we have \(\square\) (the beamsplitter) acting on standard basis states, so we can use the transformation from Section 3.2 to see how the state transforms: \[ \begin{align} \ket{\psi_2} =&\frac{1}{\sqrt{2}}\ket{0}_P\ket{H}_D+\frac{1}{\sqrt{2}}\ket{1}_P\ket{V}_D \end{align}\]
At this point, the single photon is traveling in two directions, horizontally and vertically. It is in a superposition of the two standard basis states \(\ket{H}_D\) and \(\ket{V}_D\). In this case, this corresponds to the photon being in two positions at once - literally a superposition. (This is where the term superposition comes from.)
Next the state of the photon encounters the mirrors of the interferometer. We represent the mirror with the symbol \(\textbackslash\): \[ \begin{align} \ket{\psi_3}&=\textbackslash\ket{\psi_2}=\textbackslash\left(\frac{1}{\sqrt{2}}\ket{0}_P\ket{H}_D+\frac{1}{\sqrt{2}}\ket{1}_P\ket{V}_D\right)\\ &\frac{1}{\sqrt{2}}\textbackslash\ket{0}_P\ket{H}_D+\frac{1}{\sqrt{2}}\textbackslash\ket{1}_P\ket{V}_D, \end{align} \] where we have again distributed the gate and commuted the scalars.
Now the mirror only affects the direction qubit, and it acts by exchanging the standard basis states, so we have \[ \begin{align} \ket{\psi_3}&=\frac{1}{\sqrt{2}}\ket{0}_P\ket{V}_D+\frac{1}{\sqrt{2}}\ket{1}_P\ket{H}_D. \end{align} \]
Now we again have a beamsplitter acting on our state: \[ \begin{align} \ket{\psi_4}&=\square\ket{\psi_3}=\square\left(\frac{1}{\sqrt{2}}\ket{0}_P\ket{V}_D+\frac{1}{\sqrt{2}}\ket{1}_P\ket{H}_D\right)\\ &=\frac{1}{\sqrt{2}}\ket{0}_P\ket{V}_D+\frac{1}{\sqrt{2}}\ket{1}_P\ket{V}_D\\ &=\left(\frac{1}{\sqrt{2}}\ket{0}_P+\frac{1}{\sqrt{2}}\ket{1}_P\right)\ket{V}_D\\ &=\ket{+}_P\ket{V}_D. \end{align} \]
Thus the output of this beamsplitter is a \(\ket{+}_P\ket{V}_E\), a right diagonally polarized photon traveling downwards out of the beamsplitter
[QI4]
What is the output state of the following interferometer?
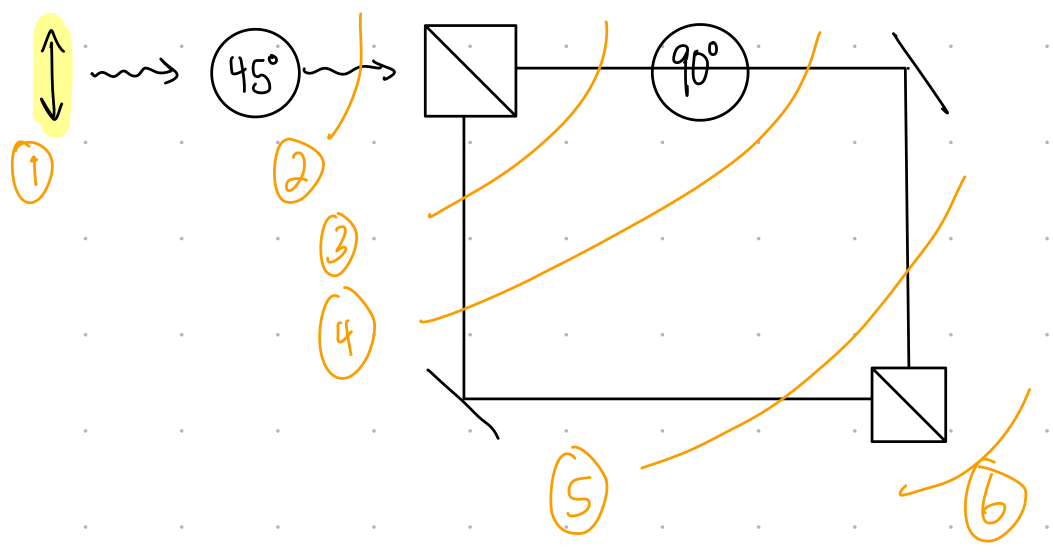
Big ideas:
- One photon takes both paths; the photon acts like a particle but also like a wave.
- Path and polarization are entangled
- Objects in the arm of the interferometer (like the \(90^\circ\) waveplate), affect the output state of the photon…so why don’t we try putting the bomb in one arm!
We’ll try to identify the bomb by putting it in the interferometer:
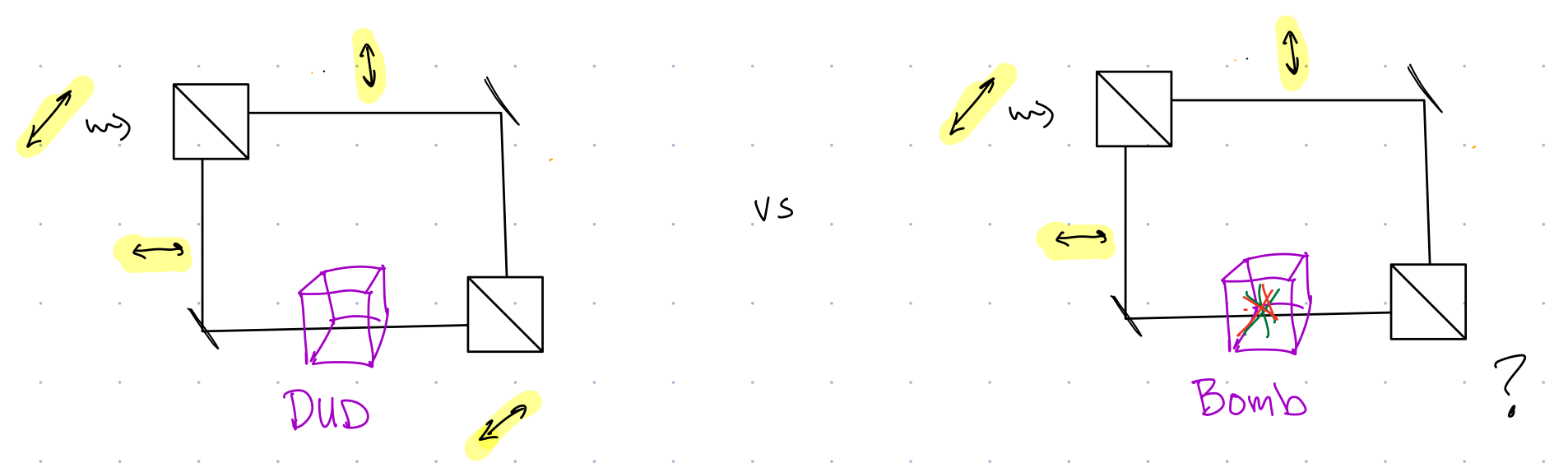
The live bomb acts like a measurement, asking the photon to decide whether it is in the upper or lower arm of the interferometer, causing a collapse of the superposition to a standard basis state. We call this a collapse of the wavefunction.
3.4 Partial Measurement
The bomb doesn’t actually cause a full measurement, but rather what is called a partial measurement.
Suppose you have a state \(\ket{\psi}_{AB}\), with two qubits \(A\) and \(B\). Further suppose you measure only the \(A\) qubit in the standard basis: \(M_A=\{\ket{0},\ket{1}\}.\) We call this scenario a partial measurement. We extract some information about the \(A\) system, while causing the state to partially collapse.
To determine the outcome of the partial measurement (the probability of each outcome, and how the state collapses in each case) we first need to write \(\ket{\psi}_{AB}\) in the standard basis: \[\ket{\psi}_{AB}=a_{00}\ket{00}_{AB}+a_{01}\ket{01}_{AB}+a_{10}\ket{10}_{AB}+a_{11}\ket{11}_{AB}. \tag{1}\] Next because we are measuring the \(A\) qubit in the standard basis, we need to group all of the \(A\) kets that have the same standard basis state (in this step we are not doing anything except re-writing Equation 1): \[\ket{\psi}_{AB}=\ket{0}_A(a_{00}\ket{0}+a_{01}\ket{1})_B+\ket{1}_A(a_{10}\ket{0}+a_{11}\ket{1})_B. \] In the above expression, we have factored out the \(A\) qubits, and commuted the scalars. Note we have kept the \(A\) and \(B\) order the same - you should never switch the order of \(A\) and \(B\) kets.
- The probability of getting outcome \(\ket{0}_A\) when we make the measurement \(M_A=\{\ket{0},\ket{1}\}\), is \(p(\ket{0})=|a_{00}|^2+|a_{01}|^2\). When we get outcome \(\ket{0}_A\), the state collapses to \(\frac{1}{\sqrt{p(\ket{0})}}\ket{0}_A(a_{00}\ket{0}+a_{01}\ket{1})_B\).
- The probability of getting outcome \(\ket{1}_A\) when we make the measurement \(M_A=\{\ket{0},\ket{1}\}\), is \(p(\ket{1})=|a_{10}|^2+|a_{11}|^2\), and the state collapses to \(\frac{1}{\sqrt{p(\ket{1})}}\ket{1}_A(a_{10}\ket{0}+a_{11}\ket{1})_B\).
It might seem like the above probabilities and collapses are arbitrary, but there is some logic behind them.
In the case of outcome \(\ket{0}_A\), note that if we were to measure both qubits each with the standard basis measurement \(\{\ket{0},\ket{1}\}\), then \(|a_{00}|^2\) is the probability of getting outcome \(\ket{0}_A\ket{0}_B\), and \(|a_{01}|^2\) is the probability of getting outcome \(\ket{0}_A\ket{1}_B\). These are the two outcomes where qubit \(A\) has state \(\ket{0}_A\), and their combined probability is \(|a_{00}|^2+|a_{01}|^2\). So it makes sense that this is the probability of getting outcome \(\ket{0}_A\) when we only make a partial measurement. (This result is also necessary in order to avoid faster than light communication, which as far as we know is not allowed in our universe.)
Next, in the case where we get outcome \(\ket{0}_A\), the state wants to collapse to a state proportional to the parts of the system that have \(A\) in the state \(\ket{0},\) namely \(\ket{0}_A(a_{00}\ket{0}+a_{01}\ket{1})_B\). But this is not a properly normalized state, so we have to normalize it. The proper way to normalize it is to divide by \(\sqrt{p(\ket{0})}=\sqrt{|a_{00}|^2+|a_{01}|^2}\).
The reasoning is similar for outcome \(\ket{1}_A\).
Partial measurement always destroys entanglement - after partial measurement the \(A\) and \(B\) qubits are never entangled.
[QC2 warmup]
Suppose we have the state \[\ket{\psi}=\frac{1}{\sqrt{10}}\ket{00}+\sqrt{\frac{4}{10}}\ket{01}+\frac{1}{\sqrt{10}}\ket{10}-i\sqrt{\frac{4}{10}}\ket{11}\] and we measure the 2nd qubit with the measurement basis \(M=\{\ket{0},\ket{1}\}.\) What is the probability of getting each outcome, and how does the state collapse in each case?
Since the state is already in standard basis form, we can next factor out the standard basis states of the second qubit: \[\ket{\psi}=\left(\frac{1}{\sqrt{10}}\ket{0}+\frac{1}{\sqrt{10}}\ket{1}\right)\ket{0}+\left(\sqrt{\frac{4}{10}}\ket{0}-i\sqrt{\frac{4}{10}}\ket{1}\right)\ket{1}.\]
Looking at the amplitudes of the \(\ket{0}\) part, we see the probability of getting outcome \(\ket{0}\) is \[\left|\frac{1}{\sqrt{10}}\right|^2+\left|\frac{1}{\sqrt{10}}\right|^2=\frac{1}{5}.\] Then the state collapses to \[\frac{1}{\sqrt{\frac{1}{5}}}\left(\frac{1}{\sqrt{10}}\ket{0}+\frac{1}{\sqrt{10}}\ket{1}\right)\ket{0}=\ket{+}\ket{0}.\]
I’ll leave it as extra practice for you to show that the probability of getting outcome \(\ket{1}\) is \(\frac{4}{5}\), and the state collapses to \[\left(\frac{1}{\sqrt{2}}\ket{0}-i\frac{1}{\sqrt{2}}\ket{1}\right)\ket{1}.\]
4 Bomb Detection
Our two qubits are polarization and path (arm/direction) (for example, we have the state \(\ket{+}_P\ket{H}_D\)). Is the bomb measuring the polarization qubit or the path (direction) qubit?
- Polarization
- Path (direction)
We now have all of the tools we need to analyze what happens when we put a bomb in the interferometer:
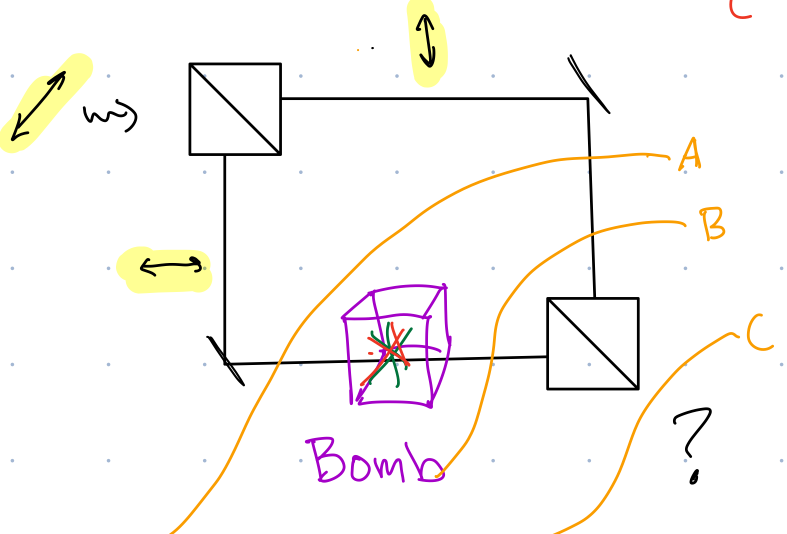
Using our standard gate transformations, we have that the state of the photon right before it encounters the bomb is: \[ \begin{align} \ket{\psi_A}=&\frac{1}{\sqrt{2}}\ket{0}_P\ket{V}_D+\frac{1}{\sqrt{2}}\ket{1}_P\ket{H}_D+0\ket{0}_P\ket{H}_D+0\ket{1}_P\ket{V}_D\\ =&\left(\frac{1}{\sqrt{2}}\ket{0}_P+0\ket{1}_P\right)\ket{V}_D+\left(\frac{1}{\sqrt{2}}\ket{1}_P+0\ket{0}_P\right)\ket{V}_D, \end{align} \] where I’ve included kets with \(0\) amplitude to make the situation more analogous to what we saw in Section 3.4
[QI4]
Use partial measurement formalism and our beamsplitter analysis tools to determine the probability that the bomb does not detonate, to determine what the photon state collapses to in the case of no detonation, and to determine what is the output state of the photon from the beamsplitter in that case.
4.1 Doing Better?
Ice breaker: Song of the summer?
What is the output state of the following interferometer?
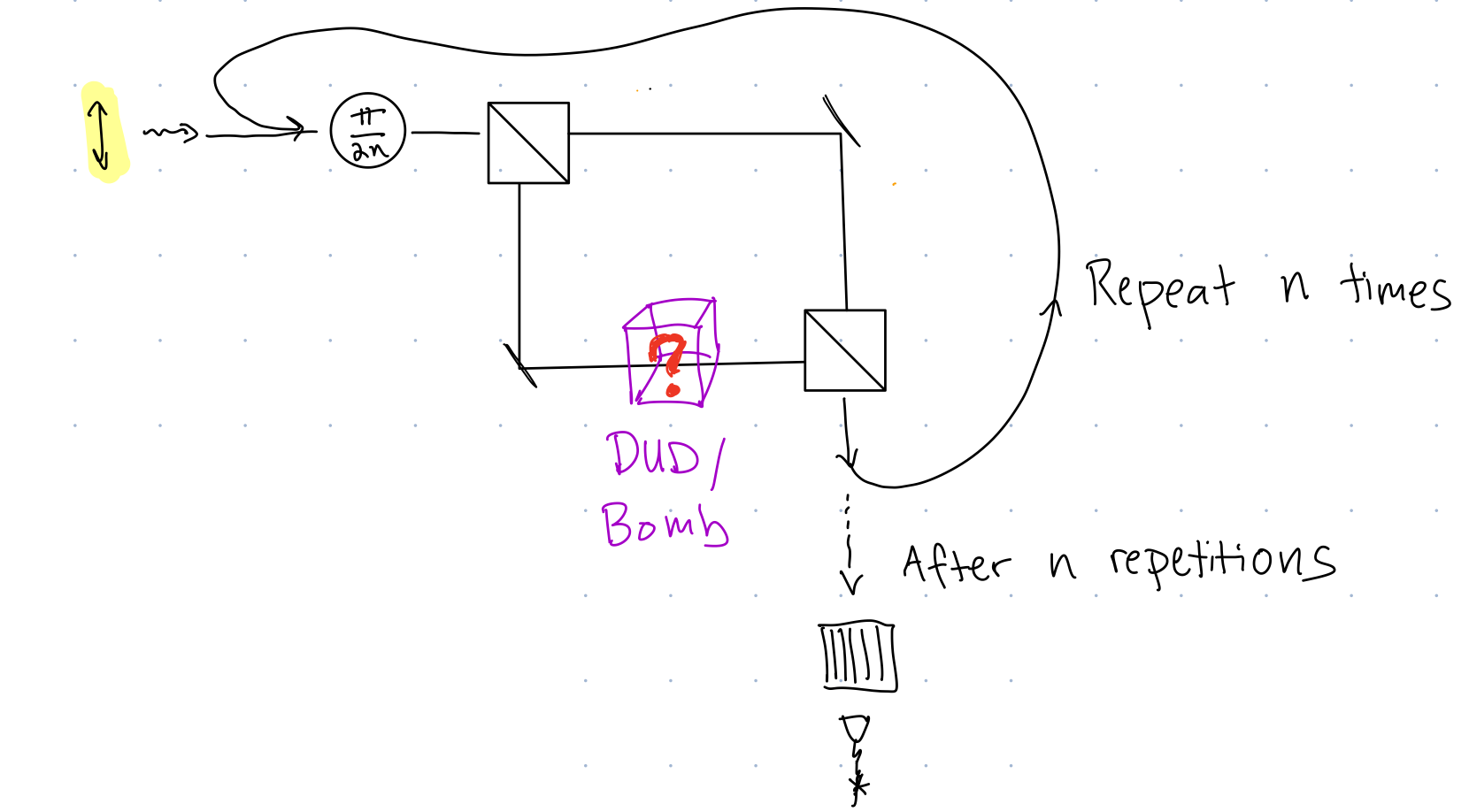
You should assume that \(n\gg 1\). (Ultimately, who ever is choosing \(n\) will have to decide on the value based on the trade-off that a larger choice of \(n\) will take more time to test, but will increase your success probability.)
Also, the \(\pi/2n\) waveplate takes \(\ket{0}\rightarrow \cos(\pi/(2n))\ket{0}+\sin(\pi/(2n))\ket{1}\), while if a photon passes through the \(\pi/2n\) waveplate \(n\) consecutive times, it acts like a \(\pi/2=90^\circ\) waveplate.
- What happens if there is a dud?
- If there is a bomb, what is the probability that there is no explosion?
- If there is a bomb and it does not explode, what is the probability that there is a detection at the single photon detector
Note that for small \(x\ll 1\):
- \(\cos(x)\approx 1-x^2/2\)
- \((1-x)^k\approx 1-kx\)