CS 467 - Lecture 12

Today we are going to play with a fairly specific physics engine that is used extensively for procedural effects -- the particle system

The particle system is essentially a special case of the system we constructed last time -- it is basically a large number of very small objects that are subject to forces in their environment

They get used to make

• fireworks
• explosions
• smoke
• flocks of birds
• water splashes
• etc...

They can also be connected together to simulate flexible surfaces like fabric or water

You may have noticed that Zach Lieberman included these in the list of things he wouldn't include in sketches because they were overused -- but they are new to you! (and too useful to dismiss, really)

There are a couple of small difference from the system we built earlier

• Particles tend to be very small, or rendered with a sprite
• Particles frequently will have a lifespan or age
• Our system will frequently include emitters which "fire" the particles out into the world
• We will include attracters and repulsers which act like something between gravity and magnetic fields

One of the questions to answer is what to do when a particle "ages out". If we are generating a lot of them, then we may be able to just reuse them immediately.

Another possibility is to store them in a pool for later use. This saves us the time required to create a new object. I bring this up because creating a pool to retain resources is a common practice in many branches in CS (managing threads in a multithreaded application is an example of this)

The other thing we should do is revisit our gravitational force

For the ball, we have the Earth, which is enormous compared to our ball. However, the reality is that as the ball is pulled towards the Earth, the Earth is also very slightly pulled towards the ball

For bodies that are similar in size, we need to consider this

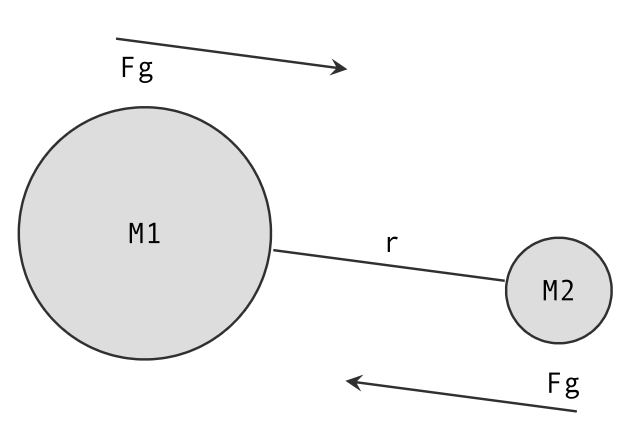
The formula is $F = \frac{Gm_1m_2}{||r||^2} \hat{r}$ The big picture here is that the force depends on the distance between the objects and it falls off following the inverse square law

$G$ is the gravitational constant, which is approximately $6.674 \times 10^{-11}$, but we can make it any number that works for us.

For our particle system, we will usually also ignore weight, so we can remove the masses from the equation

Another pragmatic change we might make is to use constrain(v, min, max) to keep the value in a sane place. Because of the amount of hand waving we do, we can end up with unreasonable values as the particles get too close together

This isn't the only way to handle attractors Another version uses

$F = \frac{1}{\sqrt{\frac{d}{r}}}$ where $d$ is the distance between the objects and $r$ is the radius of the attractor.

As long as the strength falls off with roughly the inverse square law it will look okay, and that is what we care about most here

Okay, it is your turn -- you are going to build a particle system in the next tutorial