Lecture 2 - Filtering and Convolution¶

Announcements¶

  • Please feel free to call me Scott - it has fewer syllables than "Professor" and is easier to pronounce than "Wehrwein" =)
  • Office hours are posted, but also drop in anytime my door is open or email me to make an appointment.
  • Project 1 is out today!
    • The first (and most challenging) task is to efficiently implement convolution, which you'll be qualified to do after today's lecture.
    • You'll have all the material you need by the end of tomorrow.
    • I'll do a quick demo of the project in tomorrow's class.

Goals¶

  • Know what is meant by image noise.

  • Know how to filter (v) an image by cross-correlating it with a given filter (n)/kernel/weights

  • Know how to handle image borders when filtering:

    • output sizes: full / same / valid
    • out-of-bounds values: zeros, reflection, replication

  • Get a feel for some of the image processing operations that can and can't be accomplished using linear filtering.

    • Blur, sharpen, shift

  • Know the properties of the convolution and cross-correlation, and some of their implications:

    • linearity, associativity, commutativity
    • separable filters and other compound operations

Lesson Plan¶

Revisiting image formation: image noise

Noise as motivation for neighborhood operations

Live code: mean filter

Edge handling choices:

  • full, same, valid output size
  • zero, reflect, repeat

Write down the discrete math definition; aside: write down the continuous definition

Live code: generalize to cross-correlation with filter weights

Mess with the filter weights:

  • Horizontal blur
  • Emboss

Exercise: compute a small cross-correlation result

Break

More filter weights:

  • Left shift

Convolution vs cross-correlation

Properties - shift invariance; linearity; commutativity; associativity

Filter composition using associativity

Tricks using these properties:

  • separable filters
  • Blurring sequentially
  • Sharpening
In [2]:
# boilerplate setup
%load_ext autoreload
%autoreload 2

import os
import sys

src_path = os.path.abspath("../src")
if (src_path not in sys.path):
    sys.path.insert(0, src_path)

# Library imports
import numpy as np
import imageio.v3 as imageio
import matplotlib.pyplot as plt
import skimage as skim
import cv2

# codebase imports
import util
import filtering

The autoreload extension is already loaded. To reload it, use:
  %reload_ext autoreload

Image Formation Revisited¶

How do we record light intensity inside a camera?

  • Film
  • Digital sensors

Let's make beans a little noisy.

Aside: different kinds of noise manifest differently. It's often helpful to have an accurate noise model for your imaging system - an mathematical understanding or approximation of the process that gives rise to noise.

A very common one is to have i.i.d. Gaussian noise. This means:

  • Noise is independent for each pixel
  • The mean of many samples at the same pixel will be the "true" pixel value
  • The distribution around that mean will be Gaussian
In [3]:
# don't worry about the details here, we're just adding noise to beans
beans = imageio.imread("../data/beans.jpg")
bg = skim.color.rgb2gray(beans)
bg = skim.transform.rescale(bg, 0.25, anti_aliasing=True)
bn = bg + np.random.randn(*bg.shape) * 0.05
plt.imshow(bn, cmap="gray")
Out[3]:
<matplotlib.image.AxesImage at 0x11a387ad0>
No description has been provided for this image

Brainstorm¶

If each pixel measurement is corrupted with Gaussian noise, how can we improve our guess at what the "ideal" image should have been?

In [ ]:

Idea: mean filter

Live-pseudocode:

def mean_filter(img, filter_size):
    """ Apply a square spatial mean filter with side length filter_size
    to a grayscale img. Preconditions:
      - img is a grayscale (2d) float image
      - filter_size is odd """
    H, W = img.shape
    
    hw = filter_size // 2

    out = np.zeros_like(img)
    for i in range(H):
        for j in range(W):
            avg = 0
            for fi in range(-hw, hw+1):
                for fj in range(-hw, hw+1):
                    avg += img[i+fi, j+fj]
            out[i,j] = avg / filter_size**2
In [6]:
# Look at mean_filter
plt.imshow(filtering.mean_filter(bn, 5), cmap="gray")
Out[6]:
<matplotlib.image.AxesImage at 0x11aa65640>
No description has been provided for this image

Design Decisions - edge handling¶

(whiteboard)

Edge handling:

Output size:

  • valid (only output where the whole filter overlaps the image)
  • same (output same size as input)
  • full (output everywhere the filter overlaps the image even a little bit)

For anything but valid, how do you handle when the filter hangs over the void?

  • Zero padding
  • Repeat (replicate) padding
  • Reflect padding

Is a mean filter the best we can do?¶

Another example

In [4]:
sticks = skim.color.rgb2gray(imageio.imread("../data/sticks.png"))

plt.imshow(sticks, cmap="gray")
Out[4]:
<matplotlib.image.AxesImage at 0x11a3aa000>
No description has been provided for this image
In [5]:
plt.imshow(filtering.mean_filter(sticks, 9), cmap="gray")
Out[5]:
<matplotlib.image.AxesImage at 0x11a993e60>
No description has been provided for this image

See the lattice-like artifacts? Ick. Why is this happening?

Alternatives? *

Here's one:

In [7]:
plt.imshow(cv2.GaussianBlur(sticks, ksize=(9,9), sigmaX=2), cmap="gray")
Out[7]:
<matplotlib.image.AxesImage at 0x11a9ed3d0>
No description has been provided for this image

Live code(?): implement filtering.filter

In [26]:
# test out the case of the mean filter we've been using
f = np.ones((9,9)) / (9*9)

plt.imshow(filtering.filter(sticks, f), cmap="gray")
Out[26]:
<matplotlib.image.AxesImage at 0x11c5dab40>
No description has been provided for this image
In [12]:
# don't look behind the curtain!
g = np.zeros((9, 9))
g[4,4] = 1
g = cv2.GaussianBlur(g, ksize=(9, 9), sigmaX=2)
g /= g.sum()
In [13]:
plt.imshow(filtering.filter(sticks, g), cmap="gray")
Out[13]:
<matplotlib.image.AxesImage at 0x11ad37da0>
No description has been provided for this image
In [14]:
plt.imshow(f, cmap="gray")
plt.colorbar()
Out[14]:
<matplotlib.colorbar.Colorbar at 0x11aa65250>
No description has been provided for this image
In [15]:
plt.imshow(g, cmap="gray")
Out[15]:
<matplotlib.image.AxesImage at 0x11c1d72f0>
No description has been provided for this image

How would we calculate a Gaussian kernel ourselves?¶

$$G(x, y) = \frac{1}{2 \pi \sigma^2} e^{-\frac{x^2 + y^2}{2 \sigma^2}}$$

where:

  • $x, y$ are the spatial dimensions of the filter with (0,0) in the center of the kernel
  • $\sigma$ is the standard deviation of the Gaussian, (determines how wide and flat vs tall and pointy it is)

Practicalities when calculating this in real life:

  • You generally have to choose both a kernel size and a $\sigma$.
    • For a given kernel size, you can choose sigma so it fits $\pm$ 3 standard deviations, $\sigma = (k-1)/6$
    • Or for a given sigma, the kernel size that fits $\pm$ 3 standard deviations is $k = 2*\mathrm{ceil}(3*\sigma)+1$
  • Not all the mass under the Gaussian fits in a finite kernel, so we usually renormalize the kernel so the weights sum to 1.

HW Problems 1 - 4¶

(1) $f \otimes w$ indicates the cross-correlation of image $f$ with filter $w$. Compute the following cross-correlation using same output size and zero padding. $$ \begin{bmatrix} 0 & 1 & 0\\ 0 & 1 & 0\\ 0 & 1 & 0 \end{bmatrix} \otimes \begin{bmatrix} 1 & 2 & 1\\ 2 & 4 & 2\\ 1 & 2 & 1 \end{bmatrix} $$

(2) Perform the same cross-correlation as above, but use repeat padding.

(3) Perform the same cross-correlation as above, but use valid output size.

(4) Describe in words the result of applying the following filter using cross-correlation. If you aren't sure, try applying it to the image above to gain intuition.

$$ \begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0 \end{bmatrix} $$

What else could we do with this?¶

Let's mess with filter weights to do weird stuff.

In [44]:
h = np.array([
    [-1, -1, -1, 0, 0],
    [-1, 0, 0, 0, 0],
    [-1, 0, 0, 0, 1],
    [0, 0, 0, 0, 1],
    [0, 0, 1, 1, 1]],dtype=np.float64)
plt.imshow(filtering.filter(sticks, h), cmap="gray")
# plt.imshow(np.hstack([sticks, filtering.filter(sticks, h)]), cmap="gray")
Out[44]:
<matplotlib.image.AxesImage at 0x11c1d4cb0>
No description has been provided for this image
In [27]:
h = np.array([
    [1, 0, 0, 0, 0],
    [0, 1, 0, 0, 0],
    [0, 0, 1, 0, 0],
    [0, 0, 0, 1, 0],
    [0, 0, 0, 0, 1]],dtype=np.float64) / 5
    
plt.imshow(np.hstack([sticks, filtering.filter(sticks, h)]), cmap="gray")
Out[27]:
<matplotlib.image.AxesImage at 0x11c5f06e0>
No description has been provided for this image
In [45]:
h = np.array([
    [0,  0,  0,  0,  1],
    [0,  0,  0,  1,  0],
    [0,  0,  0,  0,  0],
    [0,  -1,  0, 0,  0],
    [-1,  0,  0,  0, 0]], dtype=np.float64)

plt.imshow(filtering.filter(bg, h), cmap="gray")
plt.colorbar()
Out[45]:
<matplotlib.colorbar.Colorbar at 0x11d9d5250>
No description has been provided for this image

Break¶

Math definitions¶

Discrete cross-correlation:

$$ (f \otimes g)(x, y) = \sum_{j=-\ell}^\ell \sum_{k=-\ell}^\ell f(x+j, y+k) * g(j, k) $$

Note that $g$ is defined with (0, 0) at the center.

Turns out there's a continuous version of this too! Sums become integrals:

$$ (f \otimes g)(x, y) = \int_{j=-\infty}^\infty \int_{k=-\infty}^\infty f(x+j, y+k) * g(j, k) $$ Why $\infty$? Assume zero outside the boundaries.

Properties of Cross-Correlation¶

Convolution vs cross-correlation

Properties

  • Linearity: if $a$ is a scalar, $f$ is an image, and $g$, $h$ are filters, then: $$\begin{align*} a(f \otimes g) = f \otimes ag = af \otimes g \\ (f \otimes g) + (f \otimes h) = f \otimes (g + h) \end{align*}$$
  • Associativity $$ f \otimes (g \otimes h) = (f \otimes g) \otimes h $$
  • Commutativity? $$ f \otimes g \overset{?}{=} g \otimes f $$ Check: $$ \begin{bmatrix} 0 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0 \end{bmatrix} \otimes \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix} \overset{?}{=} \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix} \otimes \begin{bmatrix} 0 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0 \end{bmatrix} $$

Aside: The filter above (with just a 1 in the middle) is called the identity filter.

Convolution¶

A small modification to cross-correlation yields Convolution:

Cross-correlation ($\otimes$): $$ (f \otimes g)(x, y) = \sum_{j=-\ell}^\ell \sum_{k=-\ell}^\ell f(x+j, y+k) * g(j, k) $$ Convolution ($*$): $$ (f * g)(x, y) = \sum_{j=-\ell}^\ell \sum_{k=-\ell}^\ell f(x-j, y-k) * g(j, k) $$

This effectively flips the filter horizontally and vertically before applying it, and gains us commutativity.

Okay, what can we do with these properties?¶

We can blur, but can we sharpen?¶

Key question: what did blurring remove?

$I - blur(I)$

In [46]:
orig = bg
blurred = filtering.filter(bg, g)
lost = orig - blurred

plt.imshow(orig, cmap="gray")
Out[46]:
<matplotlib.image.AxesImage at 0x11dd8bfb0>
No description has been provided for this image
In [47]:
plt.imshow(blurred, cmap="gray")
Out[47]:
<matplotlib.image.AxesImage at 0x11dec91c0>
No description has been provided for this image
In [49]:
plt.imshow(lost, cmap="gray")
plt.colorbar()
Out[49]:
<matplotlib.colorbar.Colorbar at 0x11df8d790>
No description has been provided for this image

What if we add back what's lost?

In [50]:
plt.imshow(np.hstack([orig, orig + lost]), cmap="gray")
Out[50]:
<matplotlib.image.AxesImage at 0x11deac380>
No description has been provided for this image

(whiteboard - equations here for posterity)

Let $I$ be the original image, $G$ be a Gaussian blur filter, and $D$ be 2 times the identity filter. Then the filtered image $I'$ is:

\begin{align*} I' &= I + (I - (I * G))\\ &= (I + I) - (I * G))\\ &= (I * D) - (I * G)\\ &= I * (D - G)\\ \end{align*}

Visual intuition:

In [51]:
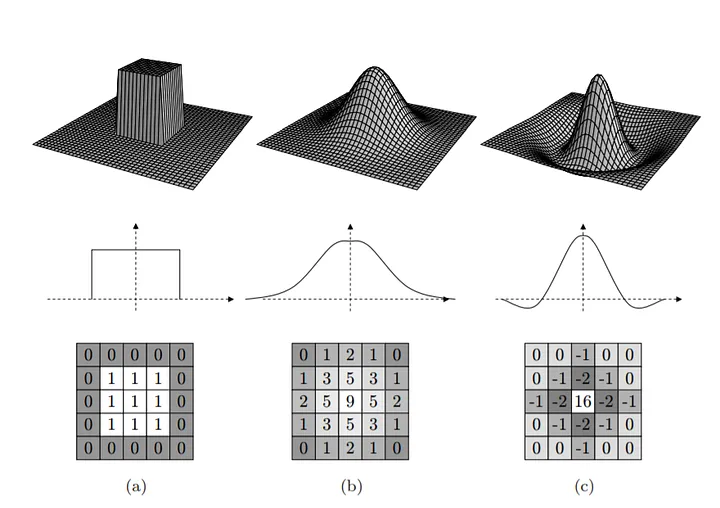
d  = np.zeros_like(g)
d[4, 4] = 2

sharp = d - g

sharpened = filtering.filter(bg, sharp)
plt.imshow(np.hstack([orig, sharpened]), cmap="gray")
Out[51]:
<matplotlib.image.AxesImage at 0x11e019640>
No description has been provided for this image

Efficiency trick: separable filters¶

Homework Problems 9-10:

  1. Compute a 3x3 filter by convolving the following $1 \times 3$ filter with its transpose using full output size and zero padding: $$ \begin{bmatrix} 1 & 2 & 1\\ \end{bmatrix} $$

  2. Suppose you have an image $F$ and you want to apply a $3 \times 3$ filter $H$ like the one above that can be written as $H = G * G^T$, where $G$ is $1 \times 3$. Which of the following will be more efficient?

  • $F * (G * G^T)$
  • $(F * G) * G^T$

Clarifying note: The two 1D filters being combined (e.g., $G$ and $G^T$ above) don't have to be the same filter!

For example, if

  • $G = \begin{bmatrix} 1 & 2 & 1 \end{bmatrix}$
  • $H = \begin{bmatrix} 1 & 0 & -1 \end{bmatrix}^T$

then

$G * H = \begin{bmatrix} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 &-2 &-1 \end{bmatrix} $, which is a funny-looking, but quite useful filter we'll see very soon!

What can't we do with convolution?¶

Homework Problem 11:

(11) For each of the following, decide whether it's possible to design a convolution filter that performs the given operation.

  • Max filter: the output pixel is the maximum value among the pixels in the input window

  • Threshold: the output pixel is

    • 255 if the input pixel is > 127
    • 0 otherwise

  • $y$ partial derivative: the output is a finite-differences approximation of the input image's vertical derivative $\frac{\partial}{\partial y} f(x, y)$.