NP
1 Learning Goals
- Describe P and NP informally, and explain why these concepts are important
- Define NP formally
- Prove a problem is in NP
2 Categorizing Problems
As computer scientists first started developing algorithms, they noticed that some problems were much easier to solve than others. Some problems seemed so hard scientists did not expect to ever be able to solve them quickly, while others problems scientists developed fast algorithms for. Researchers started categorizing problems by how quickly they could be solved.
- Easy: (These problems can all be solved relatively quickly)
- search
- sort
- multiplication
- closest points
- MWIS on a line
- most problems in this class
- Hard: (No fast algorithms could be found for these problems, and reasonable arguments can be made that it is impossible to create a fast algorithm.)
- What is the next best move in this chess game? The reason this problem seems impossible to find a fast algorithm for is that even verifying a possible solution seems ridiculously hard If someone says “QR5 is the next best move?” how could you even check that this is correct? You would have to consider every possible response from your opponent, and then every possible response you could make to every one of their responses, and so on.
Researchers noticed there was another class of problems that didn’t seem as hard as the Hard problems like playing chess, but yet they still couldn’t find fast algorithms for them like the Easy problems. These problems all had the feel of a puzzle:
- Puzzles: (In a puzzle, someone can reveal the solution to you, and you can realize “aha! that is the solution!” This is different from the chess example, where when someone gives you the solution, you can’t easily tell if it is correct or not.)
- Crossword puzzles
- Sudoku
- Finding a delivery route that takes less than k miles
- Protein folding
- Factoring numbers
- Finding a sequence of trades that will make more than k dollars
- MWIS on a general graph with weight greater than k.
Ever since scientists first started organizing problems into these categories, they have wondered if the puzzle-type problems are easy or hard. This is the essence of what is called the “P vs NP” problem. Many important real-world problems fall into the “puzzle” category, and so figuring out whether these problems are easy or hard would make a big difference in many fields of research. Also, anyone who can prove definitively that these puzzle-type problems are easy or hard will win 1 million dollars.
Note: sometimes problems that were originally in the “puzzle” category get moved to the easy category as we develop new techniques. The problem of factoring numbers is still a puzzle for regular computers, but was discovered to be easy for quantum computers. Likewise, the problem of determining whether a number is prime only recently (2002) was shown to be solvable in polynomial time.
3 P vs NP
Scientists found that they could create mathematical descriptions for the types of problems that we characterized as “Easy” (P) and “Puzzles” (NP)
Here are some informal definitions of P and NP
Definition 1 A problem is in P (Polynomial Time) if it can be solved in polynomial time relative to the input size.
Definition 2 A problem is in NP (Non-Deterministic Polynomial Time) if a solution to the problem can be checked for correctness in polynomial time relative to the input size.
Also recall the definition of polynomial time:
Definition 3 Given a problem with input size \(|x|\), we say an algorithm has polynomial runtime if it runs in \(O(|x|^c)\) for \(c\) some constant.
When computer scientists thing about these categories of problems, we often like to represent them pictorially.
We imagine a box containing all the problems in the world:
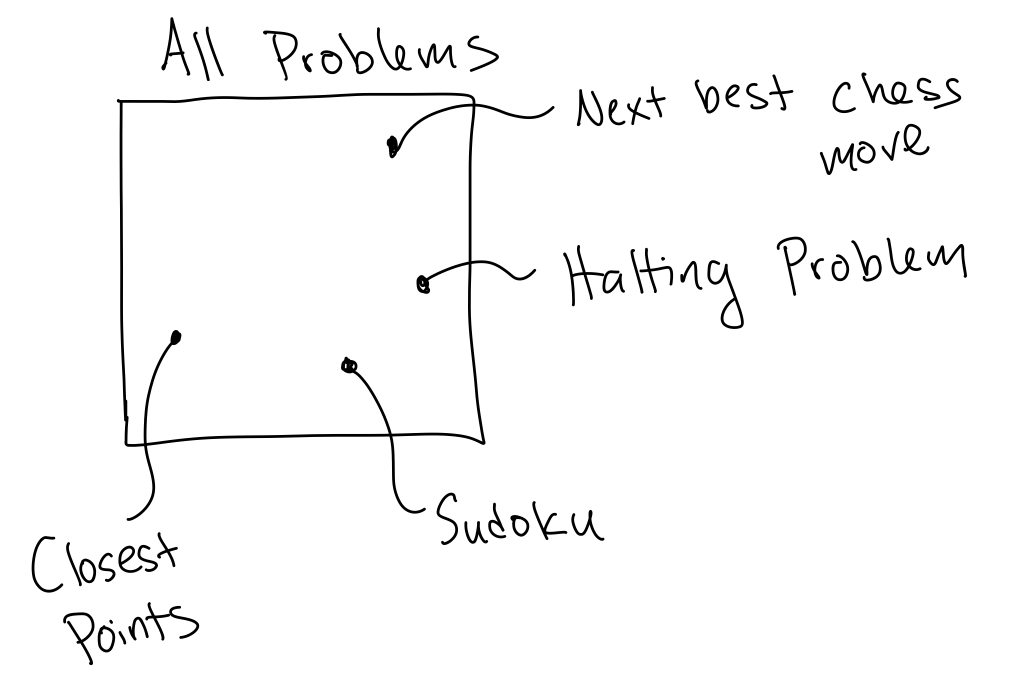
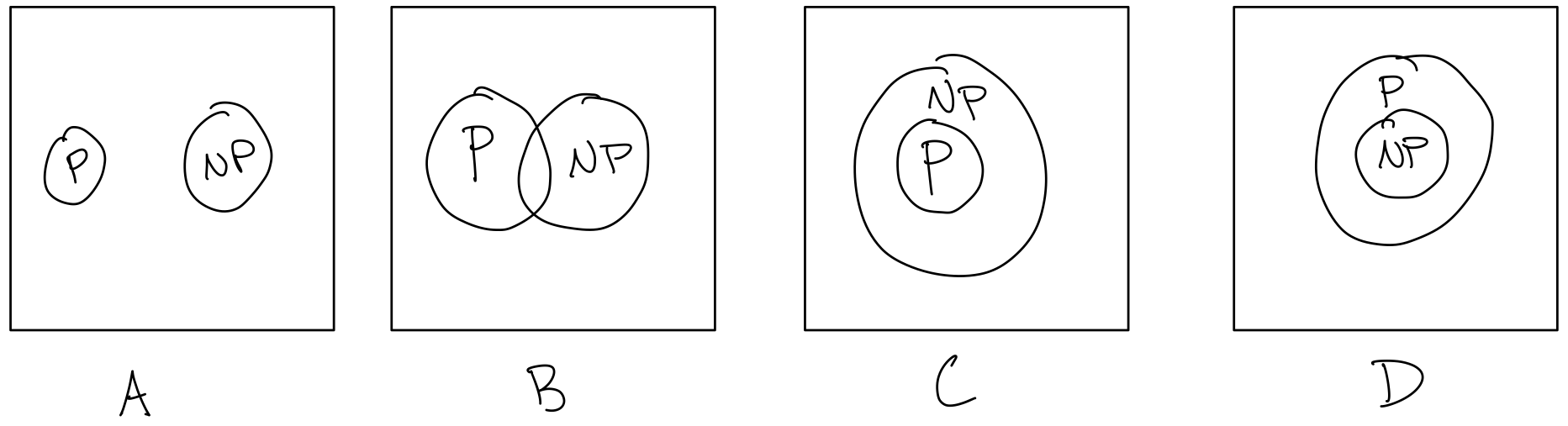
Then we can organizing the problems in this box so that all of the problems in P and NP are next to each other in space, so that we can draw a circle around all of the P problems, and another circle around all of the NP problems. Which of the following pictures is the most accurate description of P and NP?
4 Proving Problems are in NP
4.1 Definitions
We would like to be able to argue in a more formal way that a problem is in NP. To do this, we need a more formal definition than Definition 2. This is still not the most formal/precise definition, but it will be ok for this class (see CS 301, 401 for more formal definitions).
Definition 4 A problem is in NP if * Yes-No Problem * There is a polytime algorithm \(M\) such that * If \(x\) is a YES instance, \(\exists y\) such that \(M(x,y)=1\) * If \(x\) is a NO instance, \(\forall y\), \(M(x,y)=0\)
Some notes on this definition and related terminology:
- Yes-No problems are problems where the answer to the problem should be yes or no. These are also called decision problems because you are trying to make a Yes-No decision.
- \(M\) is also called the verifier because its job is to verify whether a potential solution is correct.
- \(y\) is called the witness as it is the object that you can turn to to get critical information about whether the answer should be yes or no.
- In the case of a YES instance, the witness can convince you that the answer is yes.
- For the NO instance condition, this is saying that the verifier \(M\) can’t be fooled by false witnesses. Or, we say there is no witness that will convince \(M\) that the instance is a YES instance.
An example of an NP problem is 3SAT:
Definition 5 \(x\) is a YES instance of 3SAT if it describes a Boolean formula that is an AND of ORs where each clause has at most 3 literals and there is an assignments of the variables that makes \(x\) true. Otherwise, \(x\) is a NO instance.
An instance of 3SAT is the following: \[ x=(z_1\vee z_2\vee\neg z_3)\wedge(\neg z_1\vee \neg z_3\vee z_4)\wedge(z_2\vee\neg z_5)\wedge\dots \]
Note:
- \(\wedge\) denotes logical AND
- \(\vee\) denotes logical OR
- \(\neg\) denotes logical NOT
- Variables are \(z_1,z_n,\dots, z_n\).
- Literals are \(z_1,z_n,\dots, z_n\) and \(\neg z_1,\neg z_n,\dots, \neg z_n\)
- A clause is a term inside the parenthesis.
An expected witness for 3SAT takes the form: \[ y=(z_1=T, z_2=F, z_3=F\dots) \]
Note that a witness to an NP problem can take any form, but it should be rejected by the verifier if it does not have the expected form.
4.2 Proving 3SAT is in NP
We not have all of the tools we need to prove 3SAT is in NP.
Theorem 1 3SAT\(\in\) NP
Proof. Let \(M(x,y)\) be the algorithm that checks that
- \(x\) is the AND of a series of OR clauses where each clause has at most 3 literals.
- \(y\) is an assignment of \(T\) or \(F\) to each of the \(n\) variables in \(x\)
- with the assignment in \(y\), every clause in \(x\) is true.
and outputs \(1\) if all checks pass, and outputs 0 otherwise.
We next will argue that \(M(x,y)\) runs in polynomial time in \(|x|\). We analyze the time needed to run each check:
- The algorithm can read through the formula \(x\) and as it reads through, it can verify its form. The read-through takes \(O(|x|)\) time.
- To do this check, \(M\) can ready through \(y\) and verify it has the correct form of a valid assignment. For \(y\) to be a valid assignments, the number of variables \(n\) should be less than the size of the whole formula \(x\), so reading through \(y\) should take less than \(|x|\) time. (Otherwise \(M\) can stop/halt and reject if \(y\) is going on for too long.) Thus reading through \(y\) also takes \(O(|x|)\) time.
- \(M\) can do a for loop to check each clause. Checking each clause involves looking up the values of 3 variables. There are at most \(O(|x|)\) clauses. Even if \(M\) had to read through all of \(y\) to find the values of the variables, this would only take \(O(|x|)\) time, meaning this check can be done in \(O(|x|)\) time.
Thus have shown that \(M\) runs in \(O(|x|^2)\) time, which is polynomial in \(|x|\), the input size.
Finally, if \(x\) is a YES instance that means there is a satisfying assignment, so setting \(y\) equal to the satisfying assignment will cause \(M(x,y)\) to output \(1\). If \(x\) is a NO instance, either \(x\) is not a valid formula, or it is a valid formula but there is no satisfying assignment, and no matter what \(y\) is input, at least one of \(M\)’s checks will fail and \(M\) will output \(0\).
4.3 Proving HamPath is in NP
Definition 6 \(x\) is a YES instance of Hamiltonian Path if it describes the adjacency matrix of a graph \(G\) with vertices \(s\) and \(t\), and there is a path from \(s\) to \(t\) in \(G\) that goes through each vertex once. Otherwise, \(x\) is a NO instance.
As a group show:
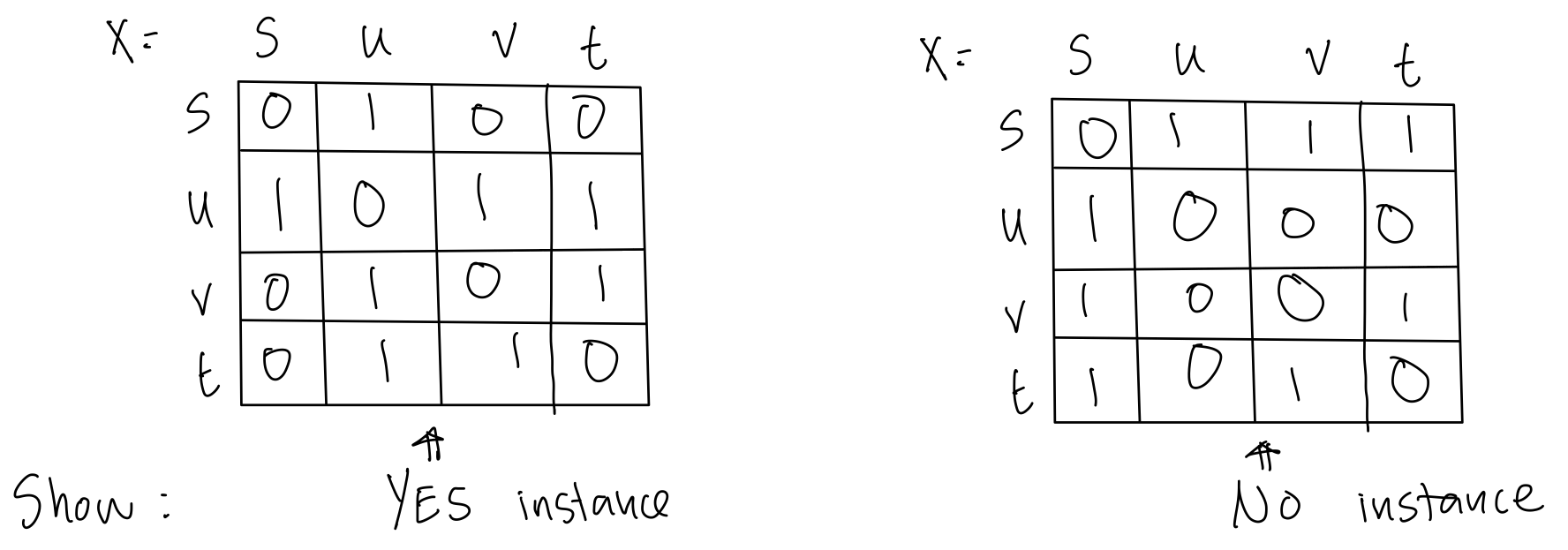
Prove: Hamiltonian Path is in NP.
Discuss: Is Knapsack in P? or NP?