Max Weight Independent Set

In-class notes

1 Learning Goals

  • Describe and benchmark Max Weight Independent Set problem
  • Create a recurrence for MWIS on a line
  • Explain why a recursive algorithm is not a good approach
  • Design a dynamic programming algorithm for MWIS on a line

2 Max Weight Independent Set

The Max Weight Independent Set us abbreviated as MWIS.

Input:

  • Graph \(G=(V,E)\)
  • Weights \(w:V\rightarrow\mathbb{Z}^+\)
G 5 5 10 10 5–10 7 7 5–7 4 4 5–4 10–7 3 3 7–3 1 1 4–1 1–7
Figure 1: An example input to Max Weight Independent Set where each number corresponds to the weight of that vertex

Output: \(S\subseteq V\) such that:

  1. If \(\{u,v\}\in E,\) then \(u\in S\wedge v\in S\) is false
  2. \(S\) maximizes \(W(S)=\sum_{v\in S}w(v)\)

First note that we are trying to maximize a function, so that should tip you off that this is an optimization problem, and you should identify \(W(S)\) as the objective function.

The condition in part (1) is common in optimization problems and is called a “constraint.” A constraint limits the set of viable outputs in some way. In our scheduling problem, there were no constraints, which meant that we could consider every possible ordering of jobs. Here the constraint means that we should only consider certain subsets of vertices.

In the case of the Max Weight Independent Set problem, the constraint enforces the independent set condition. We say that a subset of vertices of a graph is an independent set if it satisfies the constraint in (1), i.e. that no pair of vertices connected by an edge are both in the set.

We call \(W(S)\) the weight of set \(S\). Thus the name of the problem “Max Weight Independent Set” describes what we want to do: namely find the independent set that has the maximum weight.

Applications: While this problem seems a bit abstract, it surprisingly has many applications. We will study these applications (and the social impact of implementing them) in future units. Some applications are:

  • Cell tower transmission scheduling
  • Choosing franchise locations
  • Determining who to invite to your party
  • Scheduling problems

Difficulty: When \(G\) is a graph where edges are allowed between any pair of vertices, like in Figure 1, this is a very hard problem and there is no known fast algorithm. In fact it is an NP-Hard problem. We will discuss what this means in the next unit.

However, when \(G\) is a line graph like in Figure 2, there is a fast algorithm, using the Dynamic Programming framework.

G 7 7 3 3 7–3 2 2 3–2 5 5 2–5
Figure 2: An example of a line graph with vertex weights.

Testing your understanding:

For the graph in Figure 2, what is the maximum weight \(W(S)\) of the max weight independent set?

  1. 0
  2. 8
  3. 9
  4. 12

3 Developing a Recurrence for Max Weight Independent Set

Recall from your pset, when you were creating a recurrence relation for the number of \(n\)-bit strings with \(2\) consecutive ones, you thought about the final bit in the string. This final bit had two possibilities: it was either a \(0\) or a \(1.\) In each case, you could determine the number of strings with \(2\) consecutive ones by using a recursive expression. We will do something similar here.

Consider the following line graph with \(n\) vertices, where \(v_i\) is the name of the \(i^\textrm{th}\) vertex in the line:

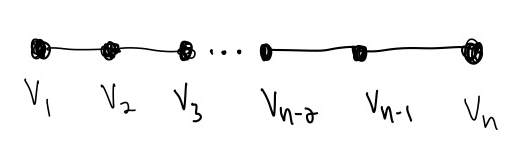
A line graph of n vertices.

There are only two possibilities for the final vertex \(v_n\) in regards to the max weight independent set \(S\):

  1. It is part of the max weight independent set, so \(v_n\in S\)
  2. It is not part of the max weight independent set, so \(v_n\notin S\)

To develop a recurrence, we need to create subproblems, so it turns out that a reasonable subproblem in this case is \(S_i\), the max weight independent set on only the first \(i\) vertices (the subgraph only including vertices \(\{v_1,v_2,\dots v_i\}\)).

Group Problem Solving

  1. If \(v_n\in S\), then \(S_n=???\)
  2. If \(v_n\notin S\), then \(S_n=???\)

You should decide what should replace the \(???\)’s in each of the above expressions. (The answer is different in each expression.) Your options are: \(S_{n-1},\) \(S_{n-2}\), \(S_{n-1}\cup \{v_n\}\), \(S_{n-2}\cup \{v_n\}\), \(S_{n-2}\cup \{v_{n-1}\}\)

Write pseudocode for a brute force approach to MWIS, and analyze the runtime.

Brainstorm how you might design a greedy or divide and conquer approach for this algorithm.

4 Recursive Approach

Once we have our recurrence relation, it suggests that a recursive algorithm is the best approach, so let’s try that:

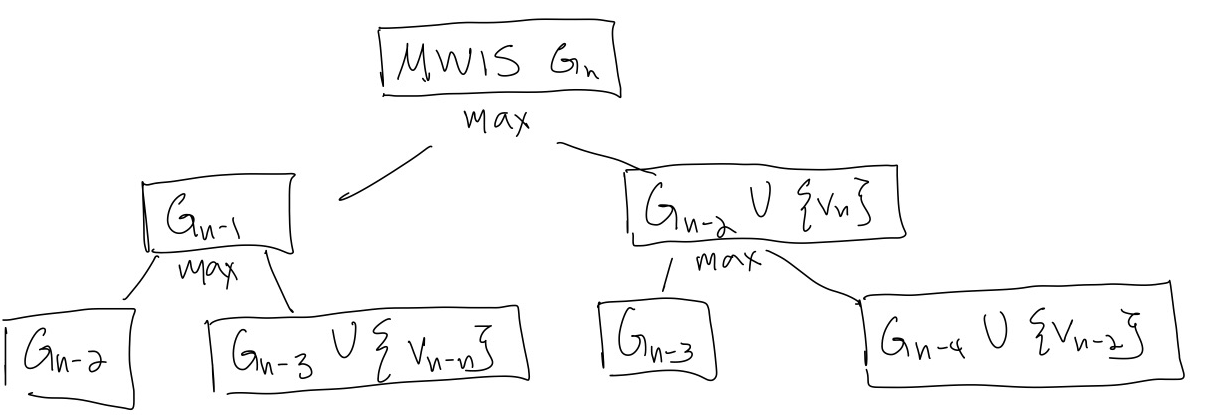
A graph showing the first few levels of recursive calls of a recursive approach to MWIS on a line

Figure 3: A graph showing the first few levels of recursive calls of a recursive approach to MWIS on a line

In Figure 3, the graph \(G_i\) is the subgraph of the first \(i\) vertices of the line graph.

However, notice that in Figure 3, at each level, the number of recursive calls increases by a factor of 2. Also, if we travel down the tree always choosing the right-most child, there will be \(n/2\) recursive calls, and if we travel down the tree always choosing the left-most child, there will be \(n\) recursive calls. Other paths will have somewhere between \(n/2\) and \(n\) recursive calls. Thus the total number of recursive calls will be \(\Omega(2^{n/2})\) (for the doubling at each level, and there being at least \(n/2\) levels.) (Here \(\Omega\), “big-Omega” is the asymptotic lower bound symbol.) Each recursive call uses at least constant time \(\Omega(1)\), so the runtime of this recursive algorithm will be \(\Omega(2^{n/2})\), which is pretty bad.

However, if we look at Figure 3, we notice that the same subproblem \(G_i\) appears in multiple recursive calls.

How many unique subproblems are there throughout the recursive algorithm?

  1. \(\sqrt{n}\)
  2. \(n/2\)
  3. \(n\)
  4. \(n^2\)

5 Dynamic Programming Approach

5.1 Storing Max Weight Independent Sets

Dynamic Programming is a paradigm to use when you want to create a recursive algorithm, but a recursive algorithm would waste time by solving the same subproblem over and over. Instead, we will store subproblem solutions in an array and look them up.

We have the recurrence: \[ S_n= \textrm{max weight set among} \begin{cases} S_{n-1}\\ S_{n-2}\cup\{v_n\} \end{cases} \tag{1}\]

The most natural approach is to create an array to store the max weight independent sets of each subproblem. So for Figure 2 we would want to fill up the following array: 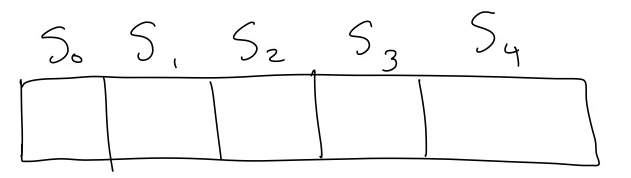5 empty connected boxes labeled S-0 through S-4

Here I have used a helpful trick, which is to start with a subproblem that contains no elements, \(S_0\).

Then we want to fill up this array from the smallest subproblem to the larget. However, if we try to use the recurrence relation in Equation 1 to solve \(S_0\), we would fall off of the bottom of the array, because there is no \(S_{-1}.\) This tells us that \(S_0\) must be a base case. But if we have a graph with no vertices, the only possible independent set is the empty set \(\emptyset.\) Next we try to use Equation 1 to solve \(S_1\), but we again fall off the bottom of the array. But if there is a graph with only one vertex, we always want to include that vertex in the max weight independent set, so \(S_1=\{v_1\}.\) Now starting at \(S_2\), we can use Equation 1, so we do not need any further base cases. For the case of Figure 2, the filled array would look like

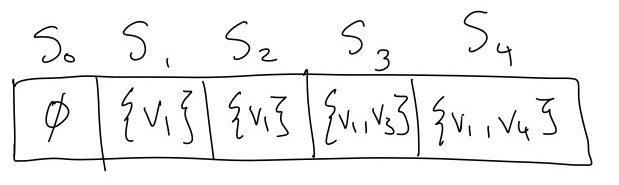
5 connected boxes labeled S-0 through S-4 and filled with sets of vertices

Figure 4: Array of boxes labeled S0 to S4, with optimal sets of vertices in each box

Combining our bases cases with our recurrence from Equation 1, we have \[ S_n= \begin{cases} \textrm{max weight set among} \begin{cases} S_{n-1}\\ S_{n-2}\cup\{v_n\} \end{cases} &\textrm{ if }n>1\\ \emptyset &\textrm{ if }n=0\\ \{v_1\}&\textrm{ if }n=1 \end{cases} \tag{2}\]

Figure 4

5.2 Storing the Objective Function Value

While you can create an algorithm that stores the optimal sets in an array, as we did in Section 5.1, this wastes time because when the set sizes get big, you will spend a lot of time copying large sets of vertices from one element of the array to the next.

To avoid this, instead of storing the optimal set for each subproblem, we will store the objective function value of the optimal set for each subproblem.

To do this, we need to create a recurrence for \(W(S_i)\), the weight of the max weight independent set for the subproblem \(S_i\).

But we looking at Equation 1, we see that we can easily translate that recurrence about optimal sets into a recurrence about the objective function value:

\[ W(S_n)= \begin{cases} \textrm{max} \begin{cases} W(S_{n-1})\\ W(S_{n-2})+w(v_n) \end{cases} &\textrm{ if }n>1\\ 0 &\textrm{ if }n=0\\ w(v_1)&\textrm{ if }n=1. \end{cases} \tag{3}\]

Now we create an array \(A\), such that \(A[i]=W(S_i)\) is the weight of the max weight independent set on \(S_i\), and we start indexing \(A\) at 0. As before, we fill up this array starting with the smallest subproblem and the moving towards larger subproblems. For the case of Figure 2, the filled array would look like \[ A=[0,7,7,9,15]. \] where the first element of \(A\) is \(A[S_0].\)

5.3 Creating an Algorithm

Now we have almost all of the pieces we need to write down the algorithm. In the pseudocode below, we first create the array \(A\) which stores the objective function values of the optimal sets. However, our algorithm should return the optimal set. To do this, we will work backwards through our array \(A\). You should figure out the missing pieces of code (???’s) in your groups.

MWIS_on_a_Line(G,w):

// Input: Graph G=(V,E) of n vertices and function \(w\) of vertex weights // Output: Independent Set of the vertices of V that have the max weight

// Create array of objective function values Initialize array A of length n+1 \(A[0]\leftarrow 0\)
\(A[1]\leftarrow w(1)\)
For \(i\leftarrow 2\) to \(n:\)
\(\quad A[i]\leftarrow\max\{A[i-1],A[i-2]+w(v_i)\}\)

// Determine optimal set
\(S\leftarrow \emptyset\)
\(i\leftarrow n\)
While \(i\geq ??\)
\(\quad \textrm{if} A[i]=A[i-1]:\)
\(\qquad ??\)
\(\quad \textrm{else}:\)
\(\qquad ??\)
Return \(S\)

Once you have filled in the missing pieces of code, step through your pseudocode (i.e. create \(A\) and \(S\) according to your pseudocoe) using the example graph Figure 5. Then analyze the runtime of your algorithm in terms of \(n\).

G 5 5 7 7 5–7 2 2 7–2 4 4 2–4 1 1 4–1
Figure 5: Another example of a line graph with vertex weights.

For most of our dynamic programming algorithms, I will not ask you to do a formal proof, but I will ask you to explain recurrence relations that you create.