Limitations of Dynamic Programming

In-class notes

1 Learning Goals

• Assess whether \(\mathbb{Z}, \mathbb{R}\), etc choices impact dynamic programming runtime correctness

2 The Problem with Real Numbers

Recall the Knapsack problem

Knapsack Problem Definition

Input:

• \(n\) items where

  • \(v_i\in \mathbb{N}\) is the value of the \(i^\textrm{th}\) item.
  • \(w_i\in \mathbb{N}\) is the weight of the \(i^\textrm{th}\) item.

• \(W\in \mathbb{N}\), the capacity, or maximum allowed weight of the knapsack.

Output: \(S\subseteq [n]\)

• \(V(S)=\sum_{i\in S}v_i\) is maximized.
  
• \(W(S)=\sum_{i\in S}w_i<W\)

Consider what the consequences would be if we have a problem where \(v_i\), \(w_i\) and \(W\) are allowed to be real numbers instead of integers?

We previously developed the following recurrence that we used to fill out our array \(A\): \[ A[n,W]= \begin{cases} \max\{A[n-1,W], A[n-1,W-w_n]+v_n\}\\ \textrm{ Base case(s)...we'll figure out later} \end{cases} \tag{1}\]

For the case of integers, for example, \(W=5\), \(n=3\), and \(w_3=2\), then to fill in \(A[3,5]\) (the 5th column of \(A\)), we would need to look at \[A[3,W-w_3]=A[3,5-2]=A[3,3]\] (the 3rd column of \(A\)).

Now suppose that \(W=5.2\) and \(w_3=2.7\). Then our recurrence relation tells us we should look at \[A[3,W-w_3]=A[3,5.2-2.7]=A[3,3.5].\] The problem is that there is no column \(3.5\) in the array \(A\). When all of the inputs were integers, we could depend on \(W-w_n\) being an integer, which meant it corresponded to a column in our array, but now we can no longer do so…

However, on the bright side, there is no problem with allowing the \(v_i\)’s to be real numbers because that would just mean that the matrix \(A\) would be filled with real numbers rather than integers.

3 Creating an Algorithm

If we have a problem with real weights, what can we do?! Instead of trying to maximize the value of the Knapsack, let’s instead just try to get a high value solution:

Knapsack \(\mathbb{R}\) Problem Definition

Input:

• \(n\) items where

  • \(v_i\in \mathbb{R}\) is the value of the \(i^\textrm{th}\) item.
  • \(w_i\in \mathbb{R}\) is the weight of the \(i^\textrm{th}\) item.

• \(W\in \mathbb{R}\), the capacity, or maximum allowed weight of the knapsack.

Output: \(S\subseteq [n]\)

• \(V(S)=\sum_{i\in S}v_i\) is close to maximized.
  
• \(W(S)=\sum_{i\in S}w_i<W\)

To solve Approximate Knapsack, please come up with a reduction from Approximate Knapsack to Knapsack:

Figure 1: Reduction from Knapsack with real inputs to Knapsack with integer inputs

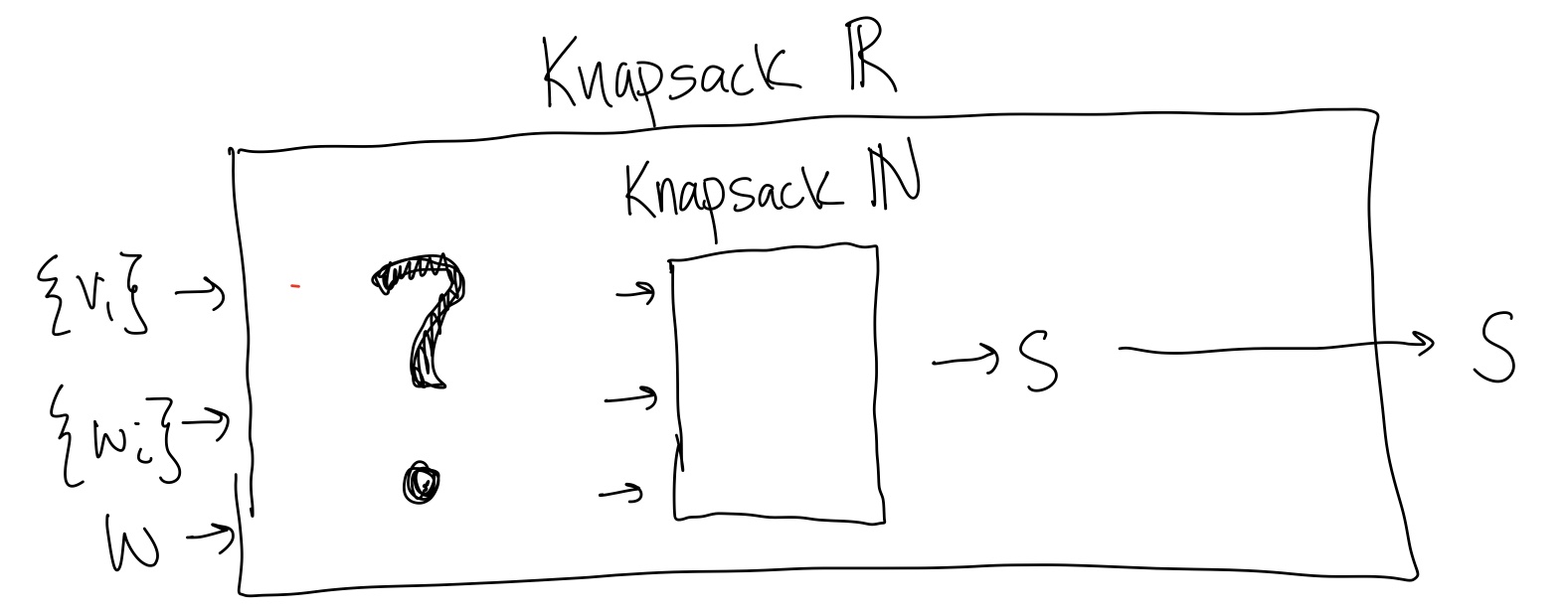
How can you improve your approximation algorithm? (At the cost of increased time.)