Closest Points 2D

In-class notes

1 Learning Goals

• Describe Closest Points Problem
• Practice analyzing ethical implications of implementation
• Practice targeting algorithm performance
• Practice reasoning (and writing proofs for) the combine step of the algorithm
• Analyze the runtime and use preprocessing to speed-up the algorithm

2 Introduction to the Closest Points Problem

2.1 Description

Input:

Assumption: No two points have the same \(x\) coordinate or the same \(y\) coordinate. For example, \((1,2)\) and \((1,4)\) would not be allowed.

Output: The distance between the two closest points in \(P\), where distance is calculated using the Euclidean distance: \[ d(p_1,p_2)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\]

2.2 Ethical Implications

The algorithm itself is essentially a mathematical object. But once it gets implemented for a particular task, it has ethical implications.

Applications of closest points (usually variants of this algorithm):

• Robotics (find the closest points between robot and environment)
• Designing roofs
• Air traffic control (identify planes that are closest together and so most likely to have a collision)

As a group please discuss the ethics of deploying an closest points algorithm for improving air traffic control. Answer the following:

• (Ice breaker) Where do you want to travel, and why?
• Who are the stakeholders in this scenario?
• Who would benefit from deploying such an algorithm?
• Who is harmed from deploying such an algorithm, and would it reinforce existing inequities?
• What additional information will you need?
• Would YOU implement this algorithm?

3 Designing an Algorithm for the Closest Points Problem

3.1 Targeting performance

Before designing a sophisticated algorithm, it is good to try to figure out what kind of performance (time complexity) we might like our algorithm to achieve. We can do this by analyzing simpler brute force approaches (worst-case) and analyzing algorithms for easier problems (best-case). We would like our sophisticated algorithm to be better than brute force, but we don’t expect it to do better than the best algorithm for an easier problem.

In your group:

• Create a simple brute force algorithm for 2D Closest Points, and analyze the big-O runtime
• Create a \(O(nlog n)\) algorithm for 1D Closest Points, and explain why it has that runtime and why it is correct.

3.2 Sketching a Divide and Conquer Algorithm:

Here is a first pass at an algorithm:

\(\texttt{CloPts}(P)\)

• Base case: we’ll do this later!

• Divide: Let’s sort the points by \(x\)-coordinates, and then divide into a left and right half. For example, if we have 6 points sorted by \(x\)-coordinate: \[P=((1,5), (2,2),(4,4), (10,20), (12,3), (19,6)) \] then we’ll divide into a left half and right half \[L=((1,5), (2,2),(4,4))\] \[R=((10,20), (12,3), (19,6)).\] We’ll call \(7\) the midline, because \(7\) is midway between \(4\) and \(10\), the \(x\)-coordinates of the two points on either side of the divide. Note that \(7\) is not literally in the middle of the space of points. The \(x\)-coordinates of the points range from \(1\) to \(19\), so if we were to just divide that space, we might get a midline of \(10\).

• Conquer:

  • \(\delta_1=\texttt{CloPts}(L)\)
  • \(\delta_2=\texttt{CloPts}(R)\)
  • \(\delta=min\{\delta_1,\delta_2\}\)

• Combine: This is too complex for this sketch…we need a new section

3.3 The Combine Step

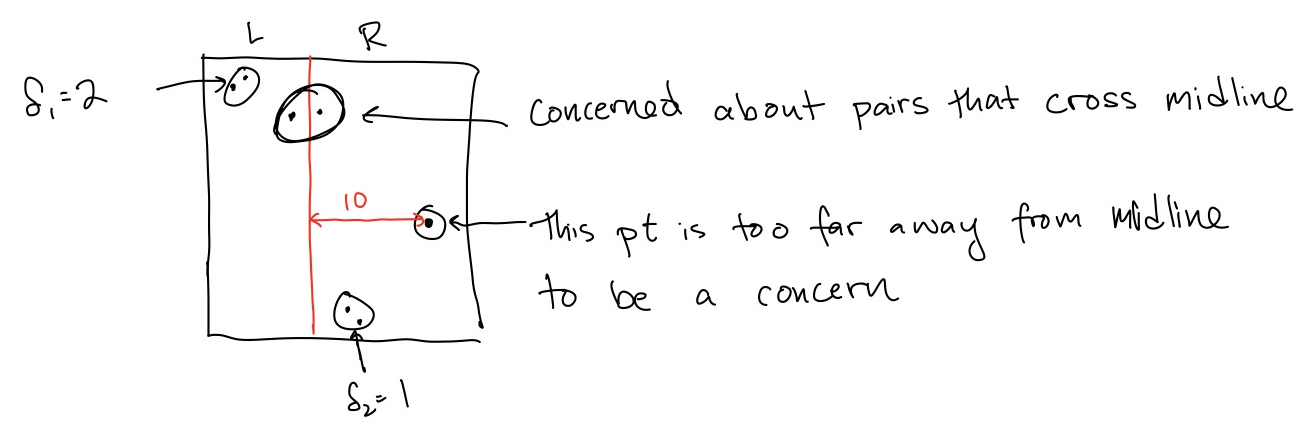
Assuming the recursive calls work correctly, we will have found the distance between the closest pair of points both on the left of the midline, and the distance between the closest pair of points both on the right of the midline, so the only thing we need to worry about is if the closest pair of points in the whole set is a pair where one point is in \(L\) and one point is in \(R\), crossing the midline.

However, it seems like points that are very far away from the midline can be ignored. As shown in the picture, if we have already found a pair in \(R\) with distance \(1\), then a point in \(R\) that is \(10\) away from the midline can’t possibly be part of the closest pair with a point in \(L\).

Recalling that \(d(p_1,p_2)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\), which points do we need to worry about in the combine step? Those within

1. \(\delta/2\) of midline
2. \(\sqrt{\delta}\) of midline
3. \(\delta\) of midline
4. \(2\delta\) of midline

To understand which is correct, we can use the following Lemma:

Lemma 1 If \(p_2\) in \(R\) is more than \(r\) from the midline, its distance to any point \(p_1\) in \(L\) is more than \(r\).

Proof. (We will give a proof sketch. A real proof can not just be equations. Need to have complete English sentences explaining the equations, and any equation should be part of a sentence, with English first, and then the equation.)

\[\begin{align} (x_1-x_2)^2&=(\textrm{ distance from }x_1 \textrm{ to midline }&+ & \textrm{distance from }x_2 \textrm{ to midline })^2\\ &\geq (0 & + & r)^2\\ &\geq r^2 && \\ ~\\ (y_1-y_2)^2&\geq 0&& \end{align}\]

\[\begin{align} (x_1-x_2)^2+(y_1-y_2)^2&\geq r^2\\ \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}&\geq r \end{align}\]

Thus we only care about checking additional points within a small distance of the midline.

If you squint, the region close to the midline almost looks like points on a line, as in the picture

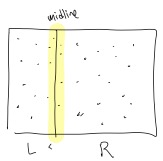
Why don’t we try using an approach similar to a line:

Combine Step
\(Y_\delta\leftarrow y\)-sorted list of points in \(P\) within \(\delta\) of midline
\(p\in Y_\delta\):
\(\quad\) Check distance from \(p\) to next ???? points
\(\quad\) Save if smallest distance found

While in our example of points on a line, we only needed to look at the next sorted point, in this case, looking at just the next point is not sufficient. To see this, consider the following picture:

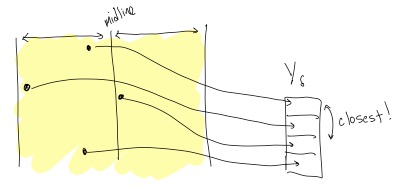
In this picture, the closest point to the top point is actually not the next point in \(Y_\delta\), but the one after that.

Lemma 2 Given a point in \(Y_\delta\), one only needs to look at the next ??? points in \(Y_\delta\) in order to find the closest point

Note that this Lemma is likely not optimal. By that, I mean that you could probably get away with checking fewer points. However, it is easy to prove!

Proof. (See post-class pdf at top of this page for picture and missing info)

Imagine dividing the region within \(\delta\) of midline into \(\delta/2\times\delta/2\) squares starting at the current point, which we call \(q\). Each of these squares can contain at most one point. To see this, for contradiction, suppose there are 2 points in a square. Then the difference in their \(x\)-coordinates is at most \(\delta/2\), and the difference in their \(y\)-coordinates is at most \(\delta/2\), so their distance is at most \[\sqrt{\left(\frac{\delta}{2}\right)^2+\left(\frac{\delta}{2}\right)^2}=\frac{\delta}{\sqrt{2}}.\] This is a contradiction, since every square contains only points in \(L\) or only points in \(R\), and we know that any two points that are both in \(L\) or both in \(R\), must have a distance of at least \(\delta\), since that is the smallest distance found in our recursive calls.

Now if we consider rows of boxes below \(q\), since each row has height \(\delta/2\), any points that are in the \(3^\textrm{rd}\) row of boxes will have a difference in \(y\)-coordinate from \(q\) that is at least \(\delta\). This means it will have a distance from \(q\) that is at least \(\delta\), and so we need not check any points in rows 3 or more below \(q\).

Thus there are only xxxx relevant boxes, and \(q\) is in one box, so there are at most ??? boxes that might contain the next closest point to \(q\), and each of these boxes contains at most one point, and all of these points would appear immediately after \(q\) in \(Y_\delta\) since \(Y_\delta\) is sorted by \(y\)-coordinate.

\(\square\)

3.4 Base Case

What size set of pts should trigger the base case?

1. \(0\)
2. \(\leq 1\)
3. \(\leq 2\)
4. \(\leq 3\)

3.5 Algorithm

Finally, we can write down the full pseudocode for the algorithm. (See post-class pdf at top of page for missing values.)

CloPts(P)
// Base Case
If \(|P|\leq ...\), then do brute force

//Divide
Sort \(P\) by \(x\)-coordinate, and then divide into arrays \(L\) and \(R\)
Pick midline to be midway between \(L\) and \(R\)

// Conquer
\(\delta=min\{\texttt{CloPts}(L),\texttt{CloPts}(R)\}\)

// Combine
$Y_$ pts within *** of midline, sorted by \(y\)-coordinate
\(\texttt{for}\) \(p_i\in Y_\delta\):
\(\quad\) \(\texttt{for}\) \(j\leftarrow i+1\) to \(i+???\):
\(\qquad\) if \(d(p_i,p_j)\leq \delta\), then \(\delta\leftarrow d(p_i,p_j)\)
return \(\delta\)

Try to explain in your own words why this is correct? What questions do you have about why this algorithm works?

4 Runtime

In groups, create a recurrence relation for the runtime of the Closest Points algorithm, using the pseudocode above.

It turns out the approach described above is not optimal. We are repeatedly sorting by \(x\) and \(y\) at each recursive step, and this adds extra factors to the runtime. Instead, we’ll presort the points before running the recursive algorithm:

** PreSort(P)
\(X\leftarrow P\) sorted by \(x\)
\(Y\leftarrow P\) sorted by \(y\)
return \(X,Y\)

CloPts(X, Y)
// Note that \(X\) and \(Y\) should contain the same set of points, just one array is sorted by \(x\) and one by \(y\).

// Base Case
1. If \(|P|\leq ...\), then do brute force

//Divide
2. Divide \(X, Y\) into \(X_L,X_R,Y_L, Y_R\), and pick midline

// Conquer
3. \(\delta=min\{\texttt{CloPts}(X_L,Y_L),\texttt{CloPts}(X_R,Y_R)\}\)

// Combine
4. Create \(Y_\delta\) from \(Y\) and midline
5. \(\texttt{for}\) \(p_i\in Y_\delta\):
\(\quad\) \(\texttt{for}\) \(j\leftarrow i+1\) to \(i+???\):
\(\qquad\) if \(d(p_i,p_j)\leq \delta\), then \(\delta\leftarrow d(p_i,p_j)\)
6. return \(\delta\)

We will go through and analyze the runtime of each step.

1. \(O(1)\)
2. This step can be done in \(O(n)\) time. \(X\) can be split by doing a loop through the elements and copying the first half in-order into \(X_L\) and copying the second half in-order into \(X_R\). \(Y\) can be split by doing a loop through the elements of \(Y\) and checking the \(x\)-coordinate of each point, and if the \(x\)-coordinate of the point is less than the midline value, copy it to the next empty spot in \(Y_L\), and if the \(x\)-coordinate of the point is more than the midline value, copy it to the next empty spot in \(Y_R\). Each of these loops only goes through \(X\) or \(Y\) one time and does constant work within each loop, so the runtime is \(O(n)\).
3. \(2T(n/2)+O(1)\), for the two recursive calls, each on an input half the size of the original, plus constant time to take the minimum
4. We again loop through \(Y\), and check the \(x\)-coordinate of each point, and if the \(x\)-coordinate of the point within \(\delta\) of the midline, we copy it \(Y_\delta\), and otherwise we do nothing with the point and just continue to the next for loop iteration.
5. Since \(Y_\delta\) can have at most \(n\) points in it, the outer loop will run at most \(n\) times. The inner for loop only iterates a constant number of times, and then the if statement only takes a constant amount of time, so the entire process takes \(O(n)\) time.
6. O(1)

Combining the contributions of each step and using big-O rules for adding runtimes, we get that the runtime is \[T(n)= \begin{cases} O(1), \textrm{ if }n\leq ...\\ 2T(n/2)+O(n), \textrm{ else} \end{cases}\] We can use the tree formula for this recurrence relation, and we find that the runtime is \(O(n\log n)\)!! This means we have achieved the same runtime as for 1-D, the best we could have possibly hoped for. Wow!

Where did we need the assumption that \(x\), \(y\) points are unique?