---
title: "Scheduling Problem"
format:
  html:
    toc: true
    number-sections: true
    code-line-numbers: true
---
[In-class notes](hand_written_notes/Scheduling1.pdf)

## Learning Goals

- Describe typical properties of greedy algorithms
- Describe the scheduling problem, as well as related terms like "objective function," "optimization problem," and "completion time."
- Design a "reasonable" scoring function and show a greedy algorithm is not optimal using a counter example
- Describe the structure of an exchange argument and prove optimality of a greedy algorithm using an exchange argument
- Modify exchange argument in the case that scoring function is not unique.
- Analyze the runtime of a greedy scheduling algorithm


## Introduction to Greedy Algorithms

There is not an agreed upon definition of greedy algorithms, and many algorithms that at first seem different from each other are all classified as greedy. Over the course of the semester we will see several examples, and this will hopefully give a better sense of what "greedy" means. However, I'll give you an informal definition 

::: {#def-greedy}
(informal definition) A greedy algorithm sequentially constructs a solution through a series of myopic/short-sighted/local/not-global/not-thinking about-the-future decisions
:::

Greedy algorithms often have the follow properties:

- Easy to create (non-optimal) greedy algorithms
- Runtime is relatively easy to analyze
- Hard to find an optimal/always correct greedy algorithm
- Hard to prove correctness 

## Scheduling Problem

### Description

For the scheduling problem, we imagine that we have a series of tasks that we want to accomplish, but we can only do one task at a time, and must complete that task before moving onto the next. Each task takes some amount of time (tasks can have the same or different times), and each task has a weight, which tells us the importance of that task. We would like to figure out how to schedule tasks to prioritize important, short tasks.
 
**Input:** $n$ tasks. Information about the tasks is given in the form of two length-$n$ arrays, one labeled $t$, and one labeled $w$. The $i^\textrm{th}$ element of array $t$ is the time required to complete the $i^\textrm{th}$ task, which we call $t_i$, and the $i^\textrm{th}$ element of array $w$ is the weight (importance) of the $i^\textrm{th}$ task, which we call $w_i$, where larger weight means more important.

**Output:** Ordering of tasks $\sigma= (\sigma_1,\sigma_2,\dots,\sigma_n)$ that minimizes
$$
A(\sigma)=\sum_{i=1}^nw_iC_i(\sigma), 
$${#eq-objective}
where $C_i(\sigma)$ is the *completion time* of task $i$ with ordering $\sigma$, described below.

We call @eq-objective the "*objective function.*" A common type of problem is an "*optimization problem,*" where the goal (object) is to determine parameters that optimize (maximize or minimize) some function, That function is called the "objective function." 

Assuming we start our first task at time $0$, then run our sequence of tasks, $C_i(\sigma)$ is the time at which the task $i$ is completed when the tasks are done in the order given by $\sigma$. For an example, suppose we have
$$
t=(3,4,2)
$$
and consider the ordering $\sigma=(3,1,2)$, so we do the third task first, then the first, and then the second. So $C_3=2$ because we do it first, it takes time $2$, so it is completed at time $2$. Next we do task $1$, but it only gets started at time $2$ after completing task $3$, and runs until time $5$, so $C_1=5.$ Now that task $1$ is completed, we can finally do task $2$ which takes another $4$ time units, and so we complete it at time $9$, so $C_2=9$. (Note, when it is clear which ordering $\sigma$ we are talking about, we will sometimes write $C_i$ instead of $C_i(\sigma)$, as we have done above.)


**Application:** Scheduling tasks on a single CPU (central processing unit) of a computer.

### Greedy Algorithm Warm-up Grab-Bag

In your groups, try to answer the following questions about greedy algorithms and our scheduling problem:

(Recall: A greedy algorithm sequentially constructs a solution through a series of myopic decisions.)

1. What is a greedy path finding algorithm on a grid? Consider the case that you would like to find the shortest path or the longest path. You can use the picture as an example: \
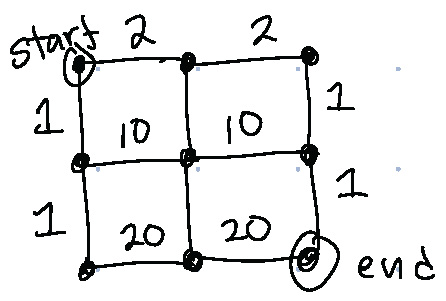![](quarto_note_pdfs/grid_graph.jpg){fig-alt="Two-by-two grid graph with weighted edges, start node in upper left corner, end node in lower right corner." width=40%}
1. Why is the following algorithm "greedy," according to the definition of greedy algorithms
   * Calculate a score $w_i-t_i$ for each task
   * Schedule tasks in order of decreasing score (highest score first)
1. Provide a counter example that the algorithm in #2 does not always minimize $A(\sigma)$. To do this:
   * Create tasks by deciding on times and weights for each task (you can get a counter example in this case with just 2 tasks)
   * Calculate scores $w_i-t_i$
   * Determine the schedule based on the scores
   * Show that this schedule is not optimal (i.e. there is a different schedule that does a better job of minimizing $A(\sigma)=\sum_iw_iC_i(\sigma)$.)
1. What might be a general ethical concern with our scheduling problem, if we decided to deploy it in any domain.
1. You determined that $w_i-t_i$ is not an optimal scoring function. Brainstorm some other potential scoring functions that would tend to prioritize important and short jobs. Explain why they seem to prioritize jobs in a reasonable way.

### Design Approach

Here is one simple greedy approach for algorithm that involve creating an order of objects:

1. Brainstorm several reasonable scoring functions.
These are "reasonable" because they all tend to prioritize jobs that are important and short, which is our goal. 
1. Test the scoring functions on examples, see how they do, and see if you can create counter examples showing a scoring function is not optimal. (In some cases, you might also be satisfied with an algorithm that is not always optimal, but is close to optimal. For example, Prof. Das in her research often tries to show that an algorithm never does worse than 90% of the optimal value of the objective function.)
1. If you can't find any counter examples, you can try to prove that your algorithm is correct.

### Proving Correctness of Greedy Scheduling {#sec-proofgreedy1}

::: {@thm-schedule}
Ordering jobs by decreasing value of $w_i/t_i$ is optimal for minimizing $A(\sigma)=\sum_iw_iC_i(\sigma)$.
:::

::: {.proof}
[We will use an "Exchange Argument," which is a type of proof by contradiction]

Assume that $w_i/t_i$ are distinct (i.e. no two jobs have the same score). Without loss of generality, we are going to relabel the tasks in decreasing score so that task $1$ has the highest score, then task $2$, etc, so that
$$w_1/t_1>w_2/t_2>w_3/t_3\dots w_n/t_n.$$
With this relabeling, we have that the greedy ordering is
$$\sigma=(1,2,3,\dots,n).$$
Assume for contradiction that $\sigma$ is not the optimal ordering. Then there must exists another ordering $\sigma^*$ that is the optimal ordering.

Since $\sigma^*\neq \sigma$, there must be tasks $b,y\in \{1,2,\dots,n\}$ where $b<y$, but $y$ appears immediately before $b$ in $\sigma^*$. In other words, $b$ and $y$ are in the wrong order, and right next to each other somewhere in $\sigma^*$, so $\sigma^*$ looks like:
$$\sigma^*=(\dots, y, b, \dots).$$
For example, if $\sigma=(1,2,3)$, and $\sigma^*=(3,1,2)$, then $3$ and $2$ are right next to each other but out of order, so we set $y=3$ and $b=1$. 

Now let $\sigma^{*'}$ be an ordering that is exactly the same as $\sigma^*$ *except* that $b$ and $y$ are exchanges (i.e. swapped). Thus $\sigma^{*'}$
looks like 
$$\sigma^{*'}=(\dots, b, y, \dots)$$
where the $\dots$ are the same sequence as in $\sigma^*$. 

Next we analyze $A(\sigma^{*})-A(\sigma^{*'})$.

[See hand written notes for analysis.]

Thus we see that $A(\sigma^{*})>A(\sigma^{*'})$. This is a contradiction because $A(\sigma^{*})$ is optimal which meant it was supposed to have the smallest $A$-value of all orderings, but instead we see that $A(\sigma^{*'}$
has a smaller $A$-value. Thus our original assumption, hat $\sigma$ was not optimal, must have been incorrect, and in fact, $\sigma$ must be the optimal ordering.
:::

## Big Picture: Exchange Argument Structure

Exchange arguments are commonly (although not always) used to prove the correctness of greedy algorithms. Here is the general structure of an exchange algorithm proof.

**Exchange Argument**

1. Let $\sigma$ be the sequence that your greedy algorithm gives you, the one that you are trying to prove is optimal. For contradiction, assume it is not optimal.
2. Then that means there is some other sequence $\sigma^*$ that is optimal.
3. But then at some point $\sigma^*$ must be out of order relative to the greedy sequence. Create a new sequence $\sigma^{*'}$ by exchanging two elements of the sequence of $\sigma^*$ to make it more like the greedy algorithm.
4. Show that $\sigma^{*'}$ is better than $\sigma^*$, a contradiction, since $\sigma^*$ was supposed to be optimal. Thus our original assumption in step 1 that $\sigma$ was not optimal must have been incorrect.


## Continuing to Analyze our Greedy Scheduling Algorithm

### Runtime of our greedy algorithm

What is the runtime of our greedy scheduling algorithm?

A) $O(1)$   
A) $O(n)$   
A) $O(n\log n)$   
A) $O(n^2)$   

### Loosening our Assumption

In our proof in @sec-proofgreedy1, we assumed that no two tasks had the same value of $w_i/t_i$. 

Where did we use this assumption in our proof?

Without this assumption, we no longer have a contradiction!! But we can modify the proof so that it still works.

::: {.proof}
[Proof sketch]
Choose some relabeling of the tasks so that
$$w_1/t_1\geq w_2/t_2\geq w_3/t_3\geq\dots \geq w_n/t_n.$$
We call $\sigma=(1,2,3,\dots,n)$ our greedy ordering.
Let $\sigma^*$ be any other ordering. Then we will show 
that $A(\sigma^*)\geq A(\sigma)$. Since we could choose
*any other* ordering for $\sigma^*$, this will show that $\sigma$ has the same or better $A$-value compared to every other possible ordering,
and thus $\sigma$ is an optimal ordering.

Consider the following sequence:
![](quarto_note_pdfs/bubbleSortSchedule.png){fig-alt="Diagram showing that a series of exchanges never increases A-value."}

By the logic of BubbleSort, if we continue to exchange out-of-order tasks, eventually we will eventually arrive at $\sigma=(1,2,3,\dots,n),$ at which point there are no further out-of-order tasks. However, at each exchange, the $A$ value of the permutation only decreases or stays the same, so we have
$A(\sigma^*)\leq A(\sigma)$. This argument works for any ordering $\sigma^*$,
so we have shown that $A(\sigma)$ is optimal.
$\square$
:::

If we no longer have the assumption that $w_i/t_i$ is unique, what is the runtime of our greedy scheduling algorithm?

A) $O(1)$   
A) $O(n)$   
A) $O(n\log n)$   
A) $O(n^2)$