--- title: "NP-Complete Problems" format: html: toc: true number-sections: true code-line-numbers: true --- [In-class notes](hand_written_notes/NPCompleteA.pdf) ## Learning Goals - Define NP-Hard and NP-Complete problems and describe their importance - Describe the parts of an NP-Complete Proof - Practice proving a problem is NP Complete (Hamiltonian Path) ## Categorizing Problems Redux We previously categorized problems into Easy (P) versus Puzzle (NP) * **P (Easy):** (These problems can all be solved relatively quickly) * search * sort * multiplication * closest points * MWIS on a line * most problems in this class * **NP (Puzzles):** (In a puzzle, someone can reveal the solution to you, and you can realize "aha! that is the solution!" This is different from the chess example, where when someone gives you the solution, you can't easily tell if it is correct or not.) * Crossword puzzles * Sudoku * Finding a delivery route that takes less than k miles * Protein folding * Factoring numbers * Finding a sequence of trades that will make more than k dollars * MWIS on a general graph with weight greater than k. But sometimes we develop new algorithmic techniques, and problems that were once thought to be hard become easy. (The best recent example of this is Primality testing.) At the same time, other NP problems, like MWIS on a general graph, have eluded any attempts to come up with an efficient algorithm. Is there a way to determine which of the problems in the NP class are really hard, and which we might be able to solve if we just come up with better techniques? One approach would be to just try to keep coming up with better algorithms, and problems that we can never seem to improve on must be the hard ones. But this is unsatisfying, since until you find an algorithm, you can't tell which is easy and which is hard. Instead, we can prove that certain NP problems are harder than others. In fact, we can prove that there are certain NP problems that are the hardest possible NP problems. (It is these very hardest problems you must address in order to win 1 million dollars in deciding P vs NP.) ## Defining the Hardest NP Problems ### NP-Hard :::{#def-nphard} A problem $Q\in \textsf{NP-Hard}$ if for every problem $R\in\textsf{NP}$, $R\leq_p Q$ ::: For example, the Halting Problem (deciding whether a particular program will halt or run forever) is in $\textsf{NP-Hard}$. This means that there is a polynomial time reduction from 3-SAT to Ham-Path, there is a polynomial time reduction from $k$-MWIS (general graph) to Ham-Path...and on and on, for every problem in NP, as shown graphically in @fig-var-reductions. 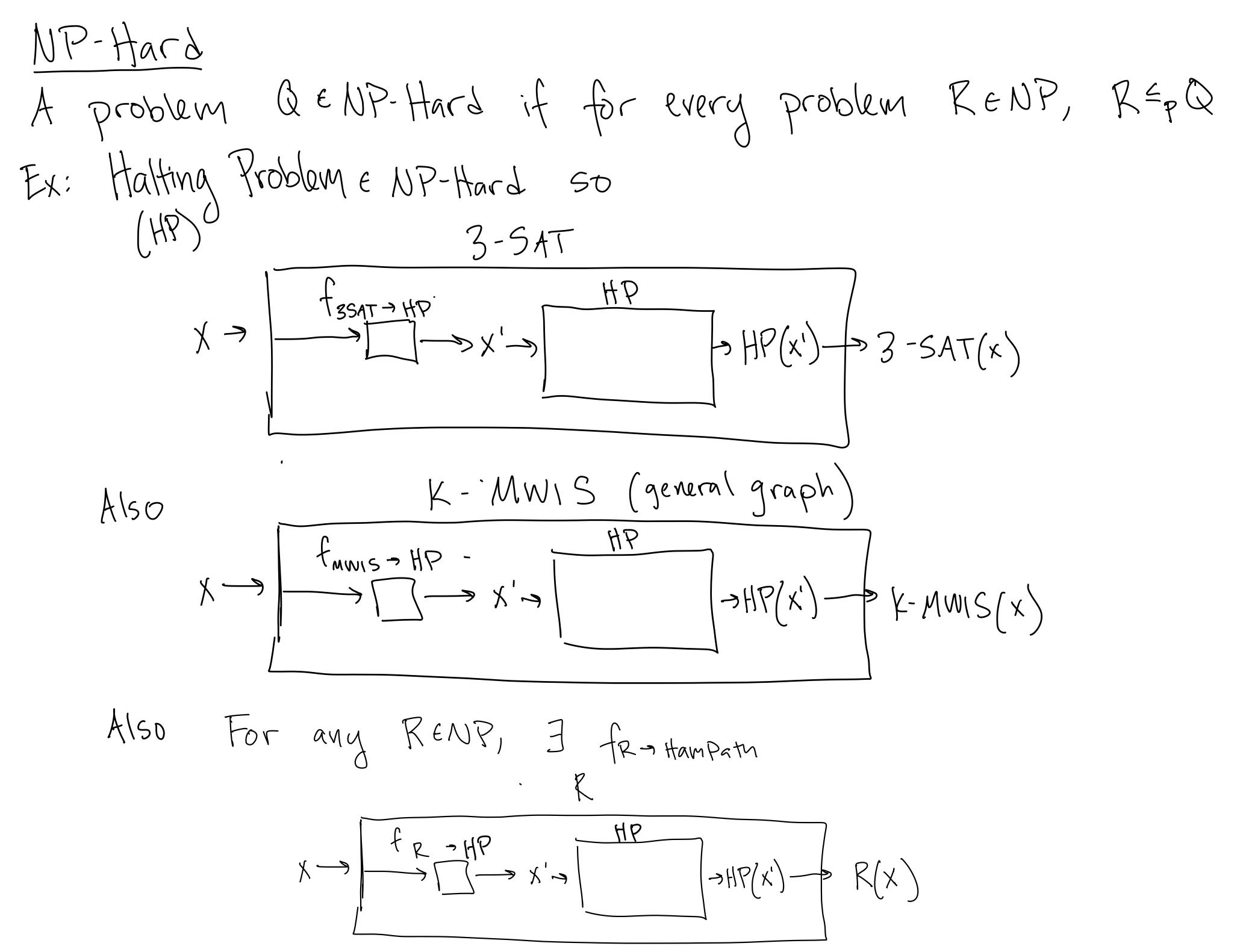![A graphical representation of several NP problems reducing to the Halting Problem](quarto_note_pdfs/VariousReductions.png){fig-alt="Graphical depictions of 3-SAT and k-MWIS being reduced to Hampath where functions are represented by boxed." width=50%, #fig-var-reductions} NP-Hard problems are called NP-Hard because if you could solve an NP-Hard problem, it would give you the power to solve all problems in NP, so this type of problem must in general be harder or require more resources than NP problems. ### NP-Complete Suprisingly, there exists problems that are in NP-Hard, but *are also in NP.* This means, that if we draw regions of different types of problems, our picture looks like @fig-containments. 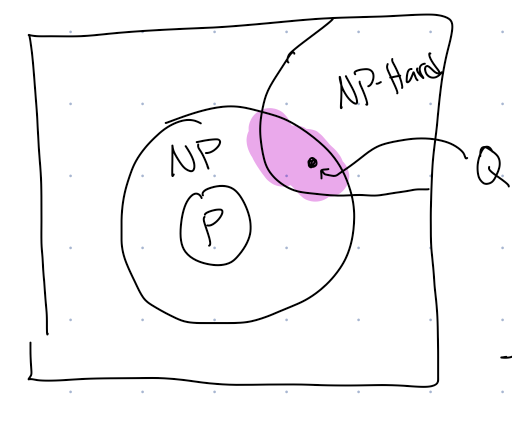![Containment picture of NP, NP-Hard, and P. The pink region is the set of NP-Complete problems.](quarto_note_pdfs/NP-HardContain.png){fig-alt="Circle labelled P inside circle labelled NP. Region labelled NP-Hard intersects with NP region." width=50%, #fig-containments} This means that some problems in NP are actually powerful enough that they can be used to solve all other problems in NP. This means that if we could come up with a fast algorithm for one NP-Complete problem, we could use it to solve all other NP problems! :::{#def-complete} A problem $Q$ is $\textsf{NP-Complete}$ if $Q\in \textsf{NP}$ and $Q\in \textsf{NP-hard}$. ::: Some $\textsf{NP-Complete}$ problems include: Hamiltonian Path, Traveling Salesperson, 3-SAT, Sudoku, etc. These are the *hardest problems in NP* and most people believe that there is no polynomial time algorithm for these problems. ## Proving a Problem is NP-Complete We will now learn how to prove that a problem is NP-Complete. We will use @prp-3SAT and @lem-doubleRed: :::{#prp-3SAT} 3SAT$\in\textsf{NP-Hard}$ ::: (You prove @prp-3SAT in 301, or at least discuss it in more detail than we have time for here.) :::{#lem-doubleRed} If $Q\in\textsf{NP-Hard}$ and $Q\leq_p R$, then $R\in\textsf{NP-Hard}.$ ::: (You will prove @lem-doubleRed in your upcoming problem set.) With these tools in hand, we can now prove: :::{#thm-Ham-Path} Hamiltonian Path is $\textsf{NP-Complete}$ ::: :::{.proof} From @def-complete, we just need to show Hamiltonian Path is in $\textsf{NP}$ and is in $\textsf{NP-Hard}$ * Hamiltonian Path is in $\textsf{NP}$ because [insert proof that Hamiltonian Path is in NP here.] (See proof in [NP Unit](NP.qmd)) * To prove that Hamiltonian Path is in $\textsf{NP-Hard}$, we will prove that 3SAT$\leq_p$Ham-Path, then using @prp-3SAT and @lem-doubleRed, we can conclude that Hamiltonian Path is in $\textsf{NP-Hard}$. We will show 3SAT$\leq_p$Ham-Path below. ::: In order to proceed, we need a slightly more rigorous definition of polynomial time reduction: :::{#def-polytime} There is a polynomial time reduction from $R$ to $Q$, denoted $R\leq_p Q$, if there exists $f_{R\rightarrow Q}:\{0,1\}^*\rightarrow \{0,1\}^*$ s.t. - There exists a constant $c_{R\rightarrow Q}$ such that the runtime of implementing $f_{R\rightarrow Q}$ on input $x$ is $O(|x|^{c_{r\rightarrow Q}}$, and - $\forall x\in\{0,1\}^*$, $x$ is a YES instance of $R$ iff $f_{R\rightarrow Q}(x)$ is a YES instance of Q ::: By @def-polytime, we see that to prove 3SAT$\leq_p$Ham-Path, we need to 1. Describe a function $f_{3SAT\rightarrow HamPath}$ 2. Show $x$ is a YES instance for 3SAT iff $f_{3SAT\rightarrow HamPath}(x)$ is a YES instance for Ham-Path 3. Show $f_{3SAT\rightarrow HamPath}$ can be implemented in polynomial time. We need a function to turn an input to 3SAT, which is a description of a Boolean formula, into an input to Hamiltonian Path, a graph. How to do this!!?? Consider the following graph. How many Hamiltonian Paths are in this graph? 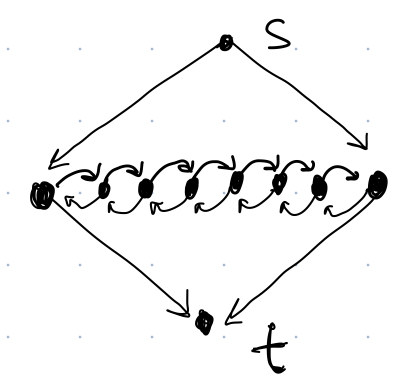![](quarto_note_pdfs/gadget1.png){width=25%} A) 2 B) 3 C) 49 D) $\binom{7}{2}$ What about in the next graph? How many Hamiltonian Paths are in this graph? 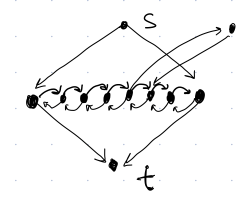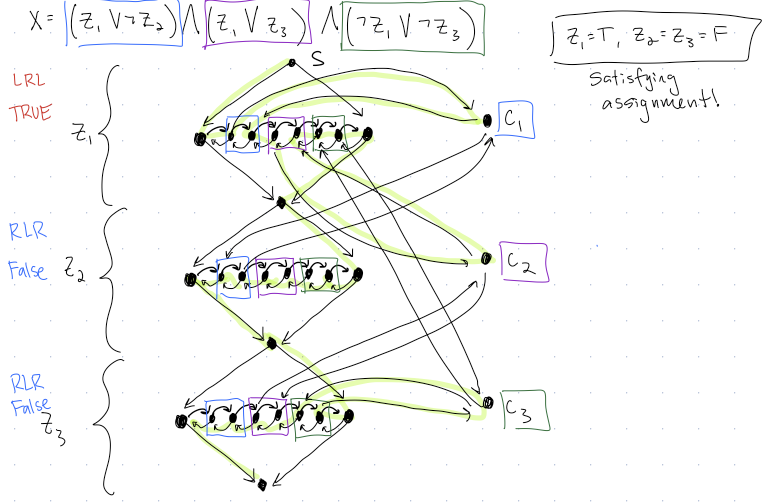![](quarto_note_pdfs/gadget2.png){width=25%} We can put link these gadgets together, one for each variable in the formula, along with one additional node for each clause, to get a graph that represents a formula: ![](quarto_note_pdfs/GraphReduction.png){width=25%} ### Group Work 1. Apply $f_{3SAT\rightarrow Ham-Path}$ to turn $x=(z_1)\wedge (\neg z_1\vee z_2)\wedge (\neg z_1\vee\neg z_2$ into a Hamiltonian Path instance. 2. What is the runtime of $f_{3SAT\rightarrow Ham-Path}$? 3. Show $x$ is a YES instance of 3SAT iff $f_{3SAT\rightarrow Ham-Path}(x)$ is a YES instance of Hamiltonian Path.