---
title: "Multi-qubit Algorithms"
format:
html:
toc: true
number-sections: true
execute:
echo: false
---
::: {.hidden}
$$
\newcommand{\braket}[2]{\langle{#1}|{#2}\rangle}
$$
:::
[Pre-class notes](HandWrittenNotes/CircuitsPre.pdf)
[In-class notes](HandWrittenNotes/QuantumCircuits.pdf)
## Learning Goals
- Describe multi-qubit algorithms using circuits and kets
## Multi-qubit Circuit Descriptions
A generic multi-qubit quantum algorithm is frequently represented as a circuit, like the following:
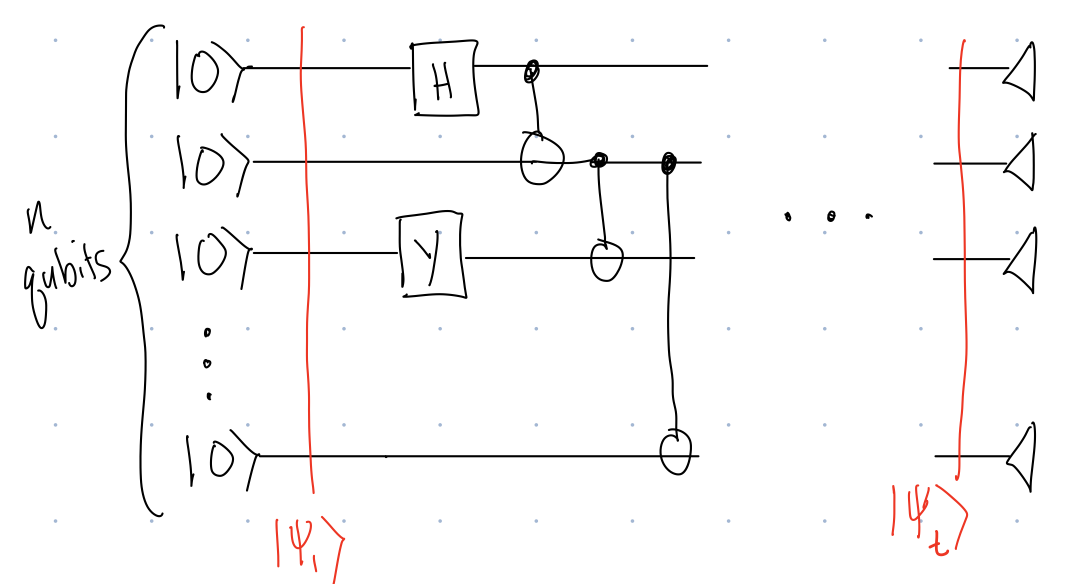{#fig-circuit}
A couple things to notice about @fig-circuit:
* There are $n$-qubits involved in the circuit, and they are all each initialized in the $\ket{0}$ state
* Over time various single and 2-qubit gates are applied to the qubits. (We will discuss why only single and two qubit gates are necessary shortly.)
* At the end of the circuit, qubits are measured in the standard basis.
Before we get further into the math/kets of analyzing such a circuit, you might be wondering how you physically implement such an algorithm.
The current top contenders for quantum computers are
- superconducting circuits, where a qubits is created from two energy levels in a superconducting ring of current, and state preparation, gates, and measurement are implemented by carefully shaped microwave pulses
- trapped ions, where a qubits is created from the hyperfine energy levels of the electons of an ion, and state preparation, gates, and measurement are implemented by shining lasers onto the ions.
Perhaps you can tell from these descriptions, but to understand these systems, you would really need to know a lot of physics, and not the physics you learn in undergrad. Luckily, at a high level, the math that describes these two very different systems is exactly the same - it is the same bras and kets we've been looking at all semester. We'll spend a little more time investigating physical implementations of quantum computers at the end of the semester.
However, physically, it is generally only possible to prepare the $\ket{0}$ state, and to measure in the $\{\ket{0}\ket{1}\}$ basis, and implement a set of single and two qubit gates, so that is how we build our circuits.
## Multi-qubit Circuit Analysis
For an $n$-qubit algorithm, the initial state of the system $\ket{\psi_1}$ can be described in several ways:
$$
\ket{\psi_1}=\ket{0}\otimes\ket{0}\otimes\cdot\otimes \ket{0}=\ket{0}\ket{0}\cdot\ket{0}=\ket{00\dots 0}=\ket{0}^{\otimes n}
$$
The first description ($\ket{0}\otimes\ket{0}\otimes\cdot\otimes \ket{0}$) is the most formal. Like with two qubits, when you combine multiple systems together, you do it mathematically with the Kronecker product, represented by $\otimes$. However, as an abbreviation, it is understood that whenever you have a ket followed by another ket, there is an implicit $\otimes$ between them, so we can write the state without all of the $\otimes$ (as $\ket{0}\ket{0}\cdot\ket{0}$). Then, we can abbreviate the state even further (in the case of all standard basis states), to put all $n$ $0$'s in a single ket, as $\ket{00\dots 0}$. Finally, if we have $n$ qubits all in the same exact state $\ket{\phi}$, we can express the state as $\ket{\phi}|^{\otimes n}$, so we can write $\ket{\psi_1}$ as $\ket{0}^{\otimes n}.$
At the end of the algorithm, the state of the system can be represented as a superposition of standard basis states:
$$
\ket{\psi_t}=\sqrt{1}{\sqrt{10}}\ket{011000}+\sqrt{\frac{2}{10}}i\ket{110101}+\sqrt{\frac{7}{10}}e^{2\pi i/3}\ket{100010}
$$
where we call $\sqrt{1}{\sqrt{10}}$, $\sqrt{\frac{2}{10}}i$, etc, the *amplitudes* of the state, and $\ket{011000}$ is a 6-qubit standard basis state.
When $n$ gets large, it gets unwieldy to write the entire state out, since there are $2^n$ possible standard basis states. So instead, we use summation notation.
A generic $n$-qubit state is written as
$$
\ket{\psi}=\sum_{s\in\{0,1\}^n}a_s\ket{s} \qquad \textrm{s.t. }a_s\in \mathbb{C}, \quad \sum_{s\in\{0,1\}^n}|a_s|^2=1
$$
- When we measure $\ket{\psi}$ in the standard basis, we get outcome $\ket{s}$ with probability $|a_s|^2$
- When we measure the first $k$ qubits of $\ket{\psi}$ in the standard basis, we get outcome $\ket{j}$ where $j$ is some $k$-bit string, with probability $\sum_{s:s=(j,..)}|a_s|^2$ (in other words, we add up the absolute value of the amplitude squared for all amplitudes of standard basis states where the first $k$ bits of the state are $j$, and the last $n-k$ bits can be anything.) And the state collapses to
$$
\frac{1}{\sqrt{\sum_{s:s=(j,..)}|a_s|^2}}\sum_{s:s=(j,..)}a_s\ket{s}
$$
(only those standard basis states where the first $k$ bits of the state are $j$, with an additional normalization factor out front to ensure the state is a valid quantum state).
## Universal Gate Set
* Classically, NOT and AND are a *universal gate set*. This means any Boolean function can be created using just AND and NOT. You could build your whole classical computer with only these two gates and nothing else. (Note that this doesn't mean that any Boolean function can be constructed *efficiently* using only AND and NOT. Some functions might take exponential time and space to implement with just AND and NOT.)
* Quantumly, CNOT, H, and T are a *universal gate set*. Where T transforms standard basis states as:
$$
\begin{align}
\ket{0}&\rightarrow\ket{0}\\
\ket{1}&\rightarrow e^{i\pi/4}\ket{1}
\end{align}
$$
For example, the X gate can be expressed as $X=HTTH$.
This is great for building a quantum computer, since it means you don't need to create infinitely many different gates, but can instead work on making sure you can implement these three gates well.
However, you might notice a problem with this. Give a set of 3 gates, we can only create countably infinitely many possible combinations, and hence only countably infinitely many gates. On the other hand, we previously discussed the fact that there are uncountably many single qubit gates. There seems to be a mismatch.
The resolution is that a universal gate set need not perfectly implement every gate:
:::{#def-universal}
**Universal Quantum Gate Set:** Given $\epsilon>0$, a universal quantum gate set an create any gate to precision $\epsilon$.
:::