Knapsack Problem

Pre-class notes

In-class notes

1 Learning Goals

  • Describe the Knapsack Problem
  • Develop recurrence for the Knapsack Problem
  • Right pseudocode for the Knapsack Problem
  • Analyze the runtime of the Knapsack Problem

2 The Knapsack Problem

Problem Definition

Input:

  • \(n\) items where

    • \(v_i\in \mathbb{N}\) is the value of the \(i^\textrm{th}\) item. å
    • \(w_i\in \mathbb{N}\) is the weight of the \(i^\textrm{th}\) item.

  • \(W\in \mathbb{N}\), the capacity, or maximum allowed weight of the knapsack.

Output: \(S\subseteq [n]\)

  • \(V(S)=\sum_{i\in S}v_i\) is maximized.
  • \(W(S)=\sum_{i\in S}w_i<W\)

Notation: \([n]\) means \(\{1,2,3,\dots, n\}\)

If you would like to have multiple items with the same value and weight, they need to be listed as separate items. For example, in the example below, if you wanted to have the possibility of adding two items both with value \(7\) and weight \(4\), you would need to add a \(5^\textrm{th}\) item with \(v_5=7\) and \(w_5=4.\)

Applications:

  • Shipping
  • Exam grading (? see pset)

Example:

Suppose the capacity \(W=5\), and the items are

Set of items input to Knapsack
item 1 2 3 4
value 6 5 8 7
weight 2 1 3 4

What is the optimal set?

  1. \(\{1,3\}\)
  2. \(\{1,4\}\)
  3. \(\{1,2,3\}\)
  4. \(\{2,3\}\)

Brute Force:

Similarly to MWIS, the brute force approach checks all possible sets and requires \(O(n2^n)\) time.

3 Dynamic Programming Approach to the Knapsack Problem

It turns out that dynamic programming gives an efficient algorithm for the Knapsack Problem.

3.1 Review of Dynamic Programming Approach:

First, let’s review the steps of developing a dynamic programming algorithm

  1. Think about the final possible options for an output

    • For example, in MWIS, we considered the final possible options of the vertex \(v_n\) being in the MWIS or not.

  2. For each option, think about how to right the solution in terms of a subproblem of the original problem, and create a recurrence

    • For example, in MWIS, we realized that after assigning the final vertex to either be in the set or not, the MWIS of the entire graph depended on the MWIS on the first \(n-1\) or first \(n-2\) vertices, and we developed the recurrence \[ S_n= \textrm{max weight set among} \begin{cases} S_{n-1} &\textrm{ if }v_n\notin S_n\\ S_{n-2}\cup\{v_n\}&\textrm{ if }v_n\in S_n\\ \textrm{Base cases} \end{cases} \tag{1}\]

  3. Convert recurrence on objects into a recurrence for the objective function

    • For the case of MWIS, we had \[ W(S_n)= \begin{cases} \textrm{max} \begin{cases} W(S_{n-1})\\ W(S_{n-2})+w(v_n) \end{cases}\\ \textrm{Base cases} \end{cases} \]

  4. Create pseudocode:

    • Create array \(A\) with a FOR loop starting from base case(s).
    • Work backwards through \(A\) to get solution

3.2 Dynamic Programming Approach to Knapsack

We’ll follow the same steps as laid out in the previous section.

  1. What is our final option?

    • Is item \(n\) part of the optimal set or not?

    1. We need to figure out what subproblems we are going to recurse on. Let’s think about what problems we will need to solve given the two final options

      • If \(n\) is not in \(S\), then it is not taking up any of our capacity \(W\), and now we are only going to consider putting items \(\{1,2,\dots, n-1\}\) in the set. So the problem is similar to what it was before, but with \(n-1\) instead of \(n\).
      • If \(n\) is in \(S\), then it is taking up some of our capacity \(W\), and so we have smaller remaining capacity to use to store additional items. In particular, the remaining capacity is \(W-w_n.\) Now in that remaining \(W-w_n\) capacity, we want to figure out with of the remaining \(n-1\) items to include. So in this case, the new effective problem we want to solve we have a modified capacity, as well as fewer items
      • Thus it makes sense to define the following subproblems: \[ S_{i,w}=S\subseteq [i] \textrm{ such that } W(S)\leq w \textrm{ and } V(S) \textrm{ is maximized} \] Given this definition, using our same example:
      Set of items input to Knapsack
      item 1 2 3 4
      value 6 5 8 7
      weight 2 1 3 4

      what is \(S_{2,4}\)?

      1. \(\{1,1\}\)
      2. \(\{1,2\}\)
      3. \(\{2,3\}\)
      4. \(\{4\}\)

    2. Using the analysis from the previous part, and our definition of \(S_{i,w}\), we see that the recurrence relation is \[ S_{n,W}= \begin{cases} S_{n-1,W} &\textrm{if } n\notin S_{n,W}\\ S_{n-1,W-w_n} &\textrm{if } n\in S_{n,W}\\ \textrm{ Base case(s)}& \textrm{we'll figure out later} \end{cases} \]

  3. Now we convert this into a recurrence relation for the objective function value. In this case, we get

\[ V(S_{n,W})= \begin{cases} \max\{V(S_{n-1,W}), V(S_{n-1,W-w_n})+v_n\}&\\ \textrm{ Base case(s)}& \textrm{we'll figure out later} \end{cases} \]

  1. Finally, we need to write pseudocode. We store the objective function values in an array \(A\). But now, because our subproblems depend on two parameters, we need a 2D array to store \(A\).

3.3 Writing Pseudocode

The first part of writing pseudocode for dynamic programming is writing code to fill in the array \(A\) from the smallest values to the largest. To build intuition we’ll try to fill out \(A\) for a particular example:

item 1 2 3
value 6 5 8
weight 2 1 3

with \(W=5.\) We have

\[ A[n,W]= \begin{cases} \max\{A[n-1,W], A[n-1,W-w_n]+v_n\}\\ \textrm{ Base case(s)...we'll figure out later} \end{cases} \tag{2}\]

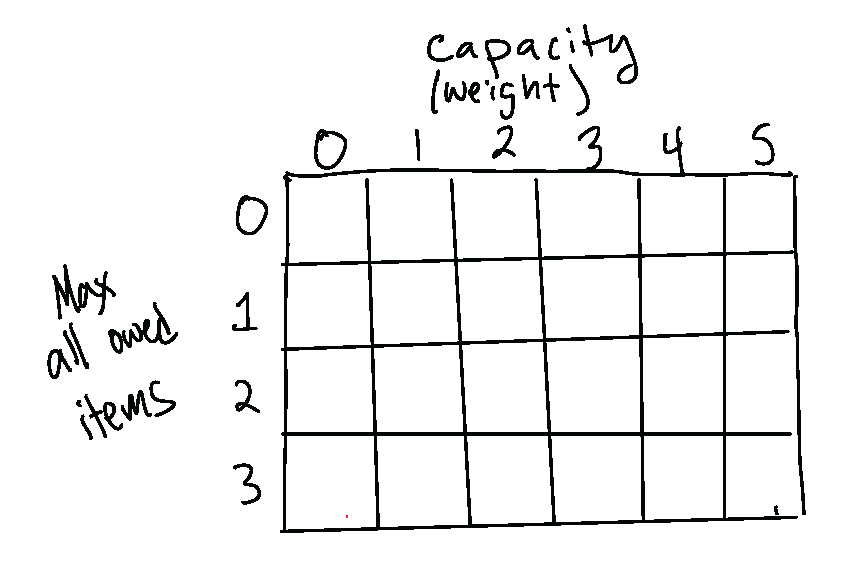
Empty grid with rows labeled by items allowed (0 through 3) and columns labeled by capacities (0 through 5)

Figure 1: Empty \(A\) array
  1. Fill out the array \(A\) in Figure 1 using Equation 2, using the 3 items above but in the process figure out
    • Base case(s)
    • Something that seems to be missing from the recurrence
  2. Next write pseudocode for working backwards through \(A\) to create the optimal set of items.
  3. If time, try to write pseudocode for filling out \(A\). (Note this code should go before the code in part 2 in your actual pseudocode.)