CS 467 - Lecture 10

Noise

We like randomness because it adds complexity and surprise into our work

We have already talked about some of the issues with using randomness directly. Randomness is too chaotic for many purposes.

There are a number of processes that seem random, but they aren't completely random -- there is a correlation between events

For example, the ridge line of a mountain is random, but any particular point is influenced by the points on either side of it

Strictly speaking, we have to acknowledge that nothing in nature is truly random -- they are complex The ridge line was formed by tectonic pressures and erosion from the weather

So, many times when we reach for randomness, we are really looking for a shortcut to approximate a complex system of forces

The problem comes because pure randomness isn't the best model Natural phenomenon have coherence on a local level

We have seen one approach to this, thinking in terms of small amounts of random variance from a pervious value

Another approach would be to use a statistical model, like a Markov chain

The solution we are going to talk about today is noise

Original and most popular form of noise is Perlin noise, created by Ken Perlin (he developed it for Tron, for which he won an Oscar)

Like our pseudorandom number generators, a noise function returns values between 0 and 1

It works by generating random numbers at fixed points in the domain and then processing the values to create a continuous function across the entire domain

We know that behind the scenes, our random number generator is really just spitting out numbers in a sequence. Imagine we could access that sequence at any point -- to look between the numbers

Generating noise

We can start by looking at a graph of random values this is also a good moment to look more closely at our inadequate random function we developed earlier

Our fake random sequence has some obvious glitches -- why?

We are going to use our fake random generator now, just because we have the ability to enter in values

Simple version

For values in between the integers, we do linear interpolation

const noise1 = (i) =>{
	const f = i % 1;
	const x = Math.floor(i);
	return lerp(fakeRandom(x), fakeRandom(x+1), f);
}

using the grapher, we can see the difference -- we went from chaos to a coherent line

it has to be admitted, however, that the spikes are unaesthetic This is caused by our doing linear interpolation between the points

Advanced version

We can make a curve that goes through the points

We can do this by varying the parameter we pass to the interpolator so it isn't linear

AS with the other curves, we are using polynomials to create this curve

We can use a Hermite interpolation $3f^2 + 2f^3$

const noise2 = (i) =>{
	const f = i % 1;
	const u = (3 - 2 * f)*f*f // Hermite interpolation "smoothstep"
	const x = Math.floor(i);
	return lerp(fakeRandom(x), fakeRandom(x+1), u);
}

Or we could use Perlin's equation $6f^5 - 15f^4 + 10f^3$

const noise3 = (i) =>{
  const f = i % 1;
  
  const u = ((6 * f - 15)* f + 10) * f * f * f; // Perlin smooth step
  const x = Math.floor(i);

  return lerp(fakeRandom(x), fakeRandom(x+1), u);
}

Multi-dimensional noise

Noise functions are frequently used to create textures, so we need them to work in multiple dimensions

To get 2D noise, imagine we have a grid of random numbers and we are interpolating from one point to another Again, we don't use liner interpolation, we will use a cubic so that we get smooth interpolation

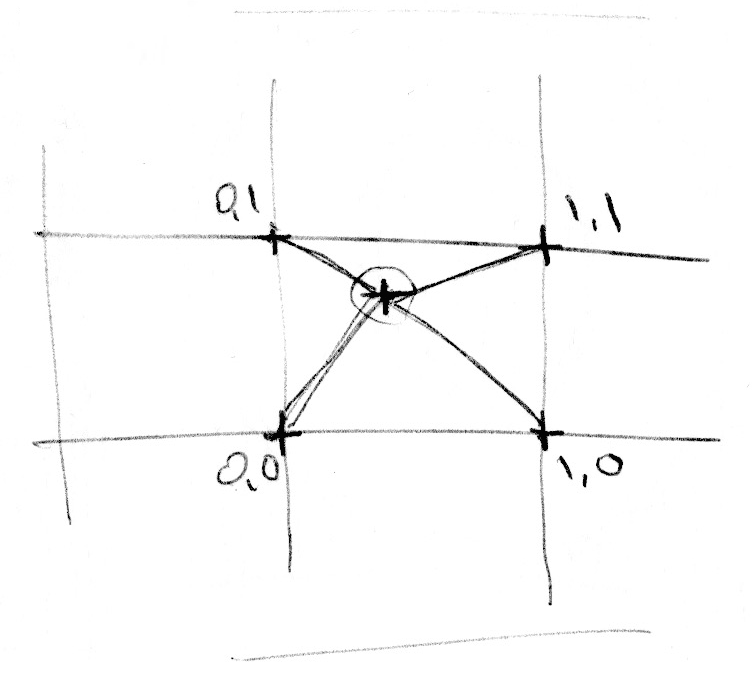(from The book of Shaders)

To get 3D noise, we will do the same, but we will be interpolating between the eight points of a unit cube

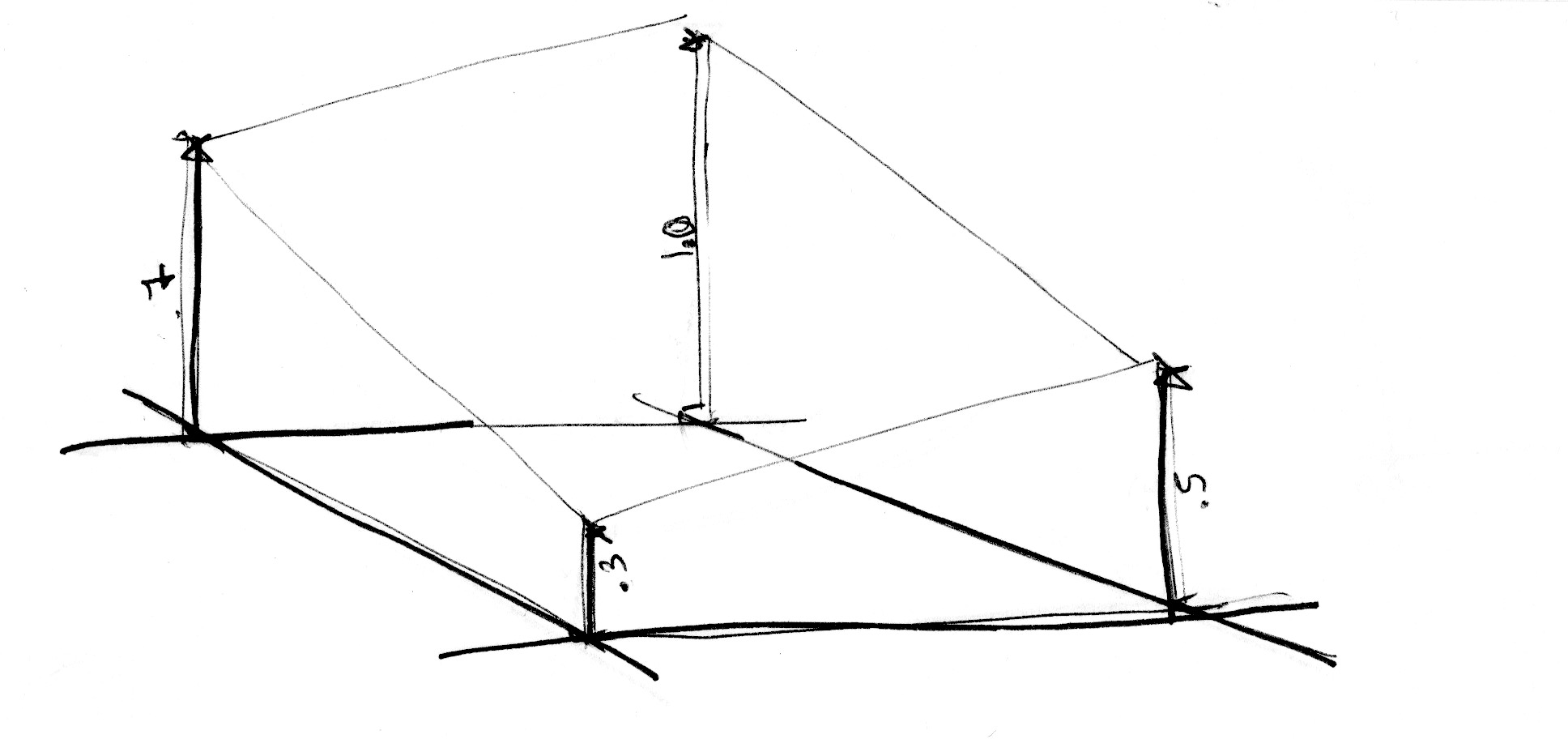(from The book of Shaders)

The benefit of these, is that we get smooth transitions in every direction

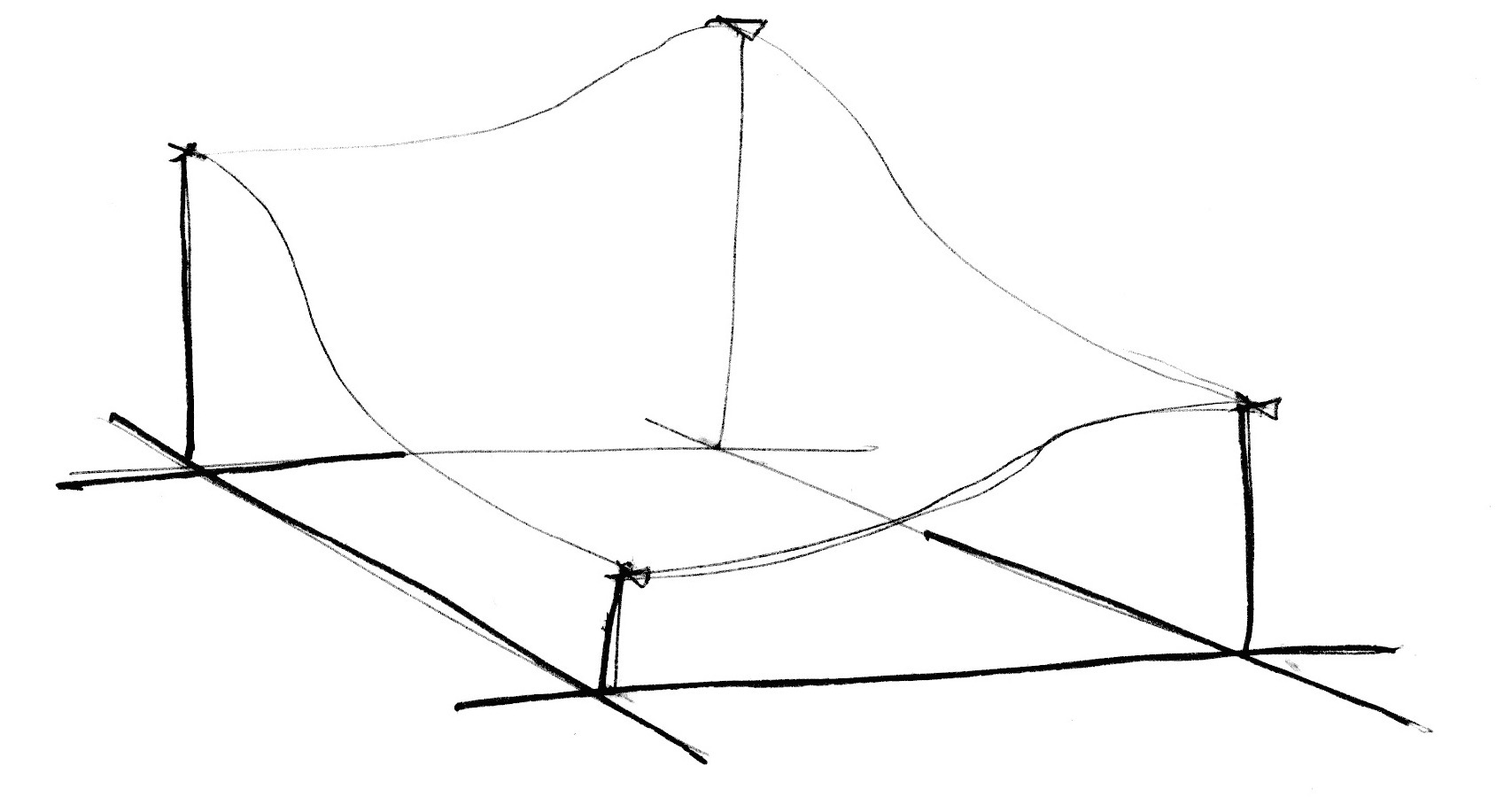(from The book of Shaders)

This approach gives us something called value noise We get a better effect with gradient noise, which interpolates gradients (basically direction vectors) instead of values

Examples

Noise field

Noise field sketch

We can start by looking at a representative of the output of the noise This is just a collection of rectangles colors using the noise function We are looking a 2D noise field -- basically just plugging in the x, y coordinates to noise() The noise function takes 1, 2, or 3 arguments to generate 1D, 2D or 3D noise

I added a feature that allows us to drag the field around so we can see it is essentially an infinite field

It isn't much to look at at this scale As we zoom in, we can see that we are getting more and more local, creating smoother transitions

Note that zooming in is done outside of the noise function, we are just scaling the x,y coordinates to cover different ranges

We also have another function for controlling the noise: noiseDetail()

To understand this, we need to realize that we can think of a random sequence as having a frequency

Noise is made up of a collection of these sequences at different frequencies, each a double of the last -- so they are referred to as octaves

By default, our noise function uses 4 octaves, each one contributing 50% less that the one before

Using noiseDetail(lod, falloff) we have some control over that

• lod - number of octaves, more gives us more detail
• falloff - how much each octave contributes relative to the one before it

Clouds

Clouds sketch

It doesn't take much to take this noise field to make clouds

Lava

Lava sketch

Changing the colors around and we can make some lava

Deforming a circle

Circle deforming sketch

Our examples up to this point have just been coloring rectangles, but we can use noise for all kinds of things, like this example that deforms a circle

Fabric

Fabric sketch

One of my favorite effects is making fabric like textures

here we just have a collection of horizontal lines that we make by making small steps with x across the page. At each point we consult the noise function with the x and y value and then permute the y position by the noise

To get the movement, we take advantage of the third argument I tend to think of this as a stack of 2D noise fields. We can move up and down between the fields, and there will be a coherence between the different levels, which gives us the relatively smooth animation

Terrain generation

Terrain generation sketch

Terrain generation is a place where we see a lot of the use of Perlin noise

Note that this isn't 3D noise -- it is 2D noise. We are using the x and y coordinates to generate a noise value, and we use the noise value as the height