Journal of Computing in Small Colleges, 13(5): 13-24, 1998
EXPERIMENTAL ANALYSIS OF POLYGON PLACEMENT PROBLEMS: AN UNDERGRADUATE RESEARCH PROJECT IN COMPUTATIONAL GEOMETRY
Cristian Dima, Greg Parent, Amy Briggs, Matthew Dickerson
Department of Mathematics and Computer Science
Middlebury College
Middlebury, VT 05753
[dima, gparent, briggs, dickerso] @middlebury.edu
Abstract: We discuss a recent undergraduate research project undertaken at Middlebury College in the summer and fall of 1997, and funded in part by a grant from the Howard Hughes Medical Institute (HHMI). Students, in collaboration with faculty advisors, were involved in the implementation, optimization, and empirical testing of recently published algorithms in computational geometry. The algorithms studied were for a set of polygon placement problems arising in robot localization, geometric tolerancing, and computer vision. Though the details of the particular algorithms may be of limited interest to those outside of the computational geometry community, the scope and goals of the research project proved to be a good model for integrating undergraduate students into original research.
NOTE:
Web sites have been developed to demonstrate our implementations and other undergraduate research projects in computational geometry. The address for the algorithms discussed here is
http://www.middlebury.edu/~math/Projects/translate.html, and work by other students in computational geometry at Middlebury College is available at http://www.middlebury.edu/classes/fall97/cx330/. As evidence of the particular suitability of computational geometry for undergraduate research, it may be noted that in this volume alone there are also four short papers (accompanying undergraduate posters at the Consortium for Computing at Small Colleges Northeastern Conference) on problems in or related to computational geometry. Web sites for these undergraduate research projects follow: "Clusters of stars java applet" (pp. 207-208) by Lilla Zollei, Mount Holyoke College: http://cs.smith.edu/~streinu/Java/Cluster/Lilla/Cluster/cluster.html; "Implementation of an algorithm for the reconstruction of rectangular visibility graphs" (p. 225) by Ling Lin, Smith College: http://grendel.csc.smith.edu/~112a-an/Projects/latest/; "Java tool for generating knots" (p. 233) by Roxana Cocan, Smith College: http://cs.smith.edu/~rcocan/Knot/index.html; and "Development of a flexible graph visualizer for parallel and sequential machines, (p. 242) by Alta Lee, Wellesley College.
1. INTRODUCTION
Computational Geometry (CG) involves the design and analysis of algorithms and data structures for the solutions to algorithmic problems of a computational nature. It has been recognized as a distinct field of computer science for a little over twenty years, during which time it has become one of the fastest growing areas of algorithmic research. Part of the interest in CG is due to its wealth of applications, including areas as far-reaching as: medical imaging, geographic information systems (GIS), robotics, computer vision, computer graphics, and computer-aided design and manufacturing (CAD/CAM). Of particular interest to us is that computational geometry is especially well-suited for undergraduate computer science education, both in the classroom curriculum and also for independent research. Many of these advantages have recently been explored by Dickerson and Drysdale in [DD98], which discusses CG in the undergraduate curriculum. In this paper, we explore instead an undergraduate research project in CG. Many problems in CG lend themselves to undergraduate research for at least the following reasons: they are simple to state yet surprisingly elegant in solution; they are highly visual, making them both easy to illustrate and also intuitive; and they make use of many interesting and fundamental data structures in computer science. Unfortunately, the undergraduate computer science teaching community has not made full use of the topics, problems, and recent research results in CG either in the classroom or for incorporating undergraduates into original research.
1.1 A Polygon Placement Problem
This paper describes an undergraduate research project in CG undertaken at Middlebury College during the summer of 1997. The project involved two undergraduate students working closely with two Middlebury faculty. Other students had previously or have since become involved in this or related projects. The main area of the research was in the optimal placement of polygons [BDP95, DS96, BBDG97]. The basic problem can be stated as follows:
There are several variants and extensions of this problem. The polygon may be convex or non-convex. The placement may be by translation only, or may also allow rotation. The problem can be extended to containment by the "annulus" region of a polygon: a strip of a given width around the boundary of the polygon, as opposed to the entire polygon interior. Yet another interesting variant is to fix the number of points to be contained and minimize the size of the polygon. Finally, the problem can be extended to polyhedra in higher dimensions. Though during the summer we concentrated on placement by translation-only in two dimensions, we were able to explore both convex and non-convex polygons, and also polygon annulus placement. By the end of the summer we were able to begin extending the work to placement by translation and rotation, and by scaling as well - an investigation that continued into the fall semester.
Additionally, the polygon placement problem is interesting in that it is very easy to state, and yet the solutions are many and varied and make use of a wealth of data structures and algorithmic techniques. It also has interesting applications to geometric tolerancing (an aspect of computer-aided manufacturing) and to robot localization. Having tangible applications was particularly motivating to an undergraduate audience. The application of the annulus placement problem to mobile robot localization can be summarized as follows. Due to errors in motion control and other conditions such as shut down or sleep, a mobile robot must periodically relocalize. Using a rangefinding device (usually laser or sonar) it takes readings of its surroundings and then must fit those readings to an environment map to determine its location. If the environment map is a polygon, this can be modeled by finding a best placement of a polygon to a set of points (the rangefinder readings), which is a variant of Problem 1. As part of this project, our team acquired a small mobile robot with sonar range finding capabilities. The research project thus promised the opportunity to test the algorithms on real world data as well as on simulated data.
For the reasons outlined above in addition to the more general advantages of Computational Geometry mentioned earlier Problem 1 proved to be an excellent problem for undergraduate research.
1.2 The Research Program
We studied these problems as a team of faculty and undergraduate students on an HHMI summer research grant. These summer research opportunities help undergraduate students to be able to conduct independent research, which is of great benefit in developing a better understanding of one’s field. Among other benefits, for example, undergraduate research is one of the best preparations for graduate work. It trains students not only in the methods of research, but also allows them to get a head start on learning about the specific area that they wish to focus on later. In the case of our project, the students were reading research-level publications and studying important algorithms in addition to work on implementation and empirical testing. They were also given the opportunity to present their results in two different forums over the course of the summer, including both a formal talk and a less formal poster presentation. These research opportunities helped especially in this way, for they funded students during the summer, when they could concentrate solely on the task that they were working on without the outside pressures of other school work.
In Section 2 we briefly describe the algorithms that we studied and how they were implemented as well as the research plan and how the students and faculty interacted during the course of the project. In Section 3 we give results of the research including comments on what aspects of the project were particularly successful. A few summary comments are made in Section 4.
2. SUMMER PLAN
We begin with a description of the summer research plan. The main goals were to study and then implement several algorithms for various polygon placement problems, and to compare their efficiency and robustness. The work was done by two student research assistants in collaboration with the faculty members. To give a sense of the type of work that we were engaged in, in this section we first describe as an example two of several algorithms that were implemented during the course of the summer. These algorithms are competing approaches to Problem 1, the Polygon Placement Problem defined in Section 1. The two algorithms that we present to solve this polygon placement problem are a line sweep and a so-called "anchored sweep"—variants of an important technique in computational geometry. Both methods also make use of several important data structures, including priority queues and a balanced binary search tree known as a "segment tree". Readers interested in more background on computational geometry are referred to [PS85,O'R94,BKOS97]. Details of these particular algorithms may be found in [BDP95,DS96,BBDG97].
After describing the algorithms, we comment on the roles of the faculty and students in the project, on the faculty-student interaction during the summer, and on how the student researchers interacted with the broader science research community during the course of the summer research program at Middlebury College.
2.1 Algorithms and Implementation
We now describe two competing approaches to Problem 1. Both approaches take as input a convex polygon and a set of points in the plane, and produce as output a translation of that polygon containing a maximum number of points, and a list of the points contained. The first algorithm uses a standard "line sweep", sometimes also called a "plane sweep". The second approach uses an "anchored sweep", and a technique known as bucketing for storing the points. The algorithms require O(nklog(nm)+m) and O(nklog(km)+m) respectively, where n is the number of points, m is the size of the polygon (the number of vertices) and k is the size of the output - that is, the number of points contained in the optimal placement.
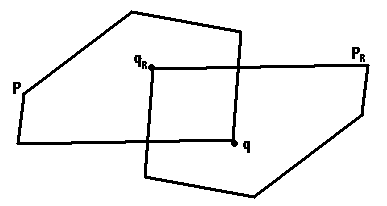
Some notation will first be helpful. Let P be a polygon. We let PR be a reflected copy of P, created by reflecting the original polygon P around the origin (or, equivalently, rotating it by
p ). We assume also that polygon P is represented as an ordered list of vertices with some initial vertex p1. To place a copy of P on point q means to translate P so that vertex p1 coincides with point q. The following observation, which follows from simple vector arithmetic, will be helpful.Observation 1: (See Figure 1.) Let PR be a reflected copy of P. Then a copy of PR placed at point qR will contain point q if and only if a copy of P placed at q contains qR.

Figure 1: Polygon P at q and rotated polygon PR at qR.
2.1.1 Line Sweep
The line sweep is one of the most common algorithmic techniques in computational geometry. (See, for example, [BKOS97, pp. 19-29].) Conceptually, it involves taking a line oriented in a fixed direction (usually horizontal or vertical), and moving ("sweeping") it across the plane. In particular, the algorithm uses a priority queue to determine the next event to be intersected by the sweeping line. Events are processed as the line hits them. The requirement is simply that all important events must be generated and added to the queue before the sweeping line actually reaches them.
A line sweep solution to Problem 1 could proceed as follows. Given a polygon P, we construct a reflected copy PR of P and place a copy of PR at each point in the input set. Suppose that some subset of k multiple copies of PRplaced at points q1,...,qk have a common intersection. If we now place a copy of the original polygon P in this intersection, then by Observation 1, this translation of P will contain those points q1,...,qk. In other words, in the arrangement of all the n copies of PR, we are looking for the point of greatest "depth" - that is, the point where the largest number of copies intersect.
Algorithmically, then, we have two steps. First, in O(m+n) time we construct PR from our input polygon P, and place a copy at each of the n points in our set. Second, we do a "line sweep" across the plane looking for the place of maximum depth in this arrangement. The line sweep keeps track of all copies of PR. An "event" in the line sweep is the start of a polygon, the end of a polygon, a polygon vertex, and an intersection between polygons. Our first data structure, a priority queue, keeps track of these events. We use a second data structure called a "segment tree" - a type of balanced binary search tree - to keep track of all polygons active at each discrete event in the event queue. In our case, the segments are polygon edges. The segment tree keeps track of the current depth between each pair of segments, updating the depth at each event and keeping a pointer to the maximum depth visited so far. Since there are n copies of the polygon, each with m vertices, we have nm total polygon vertices as events. However, if we divide the polygon into an upper "chain" and a lower "chain", and deal with entire chains rather than individual edges, we can simplify to just 2n total events of this type. It has been shown that the number of intersections between polygons is bounded by O(nk), where k is the maximum depth. Hence the total number of events of all kinds is O(nk). We must maintain two data structures. Our event queue requires time O(lognk) per event, since it is of maximum size O(nk). This simplifies to O(logn) since n
³ k. Our segment tree has maximum size 2n and also requires O(logn) time per operation. An additional O(logm) time per event is needed to find the next intersection between two polygonal chains of size O(m). So the total running time of this method is O(nklog(mn)+m).
2.1.2 Anchored Sweep
A second approach uses a slightly different sweep technique for a small improvement in asymptotic running time when k is large. We observe that for the line sweep of the previous section, all of the polygons are initially placed in the event queue, and thus the queue has initial size n even if there were no intersections between polygons. The second approach tries to avoid that situation by doing a more local sweep. The idea is to place a copy of the polygon P on a single input point q1, and to slide (or "sweep") P around q such that the boundary of P is always in contact with q1. Specifically, we sweep P all the way around q1 back to its initial position, keeping track at each instant of the number of points (in addition to q1) contained by the current translation of polygon P. This gives the set of all placements of P that must be in contact with q1. We then repeat this process for each additional point qi to determine the best overall placement. This process has been called an "anchored sweep".
Where the advantage comes is that for each point qi, we need consider only those other points within a certain distance of qi. We can accomplish this by "bucketting", another important technique in computational geometry. Let R be the smallest rectangle containing polygon P. We divide the plane into rectangular "buckets" of size (and orientation) R. Each point is placed into its appropriate bucket. Then, for the anchored sweep around a point qi, we need consider only those points in the same bucket or in one of the eight neighboring buckets including the diagonal neighbors. It is easy to show that the number of points in any region of nine neighboring buckets does not exceed O(k) where k is the maximum number of points that can be contained. Thus the number of events in each anchored sweep is O(k), and we have O(n) such sweeps. The total running time of the anchored sweep approach is O(knlog(mk)+m). It is also advantageous in that the space required drops from O(nk+m) to O(n+m).
2.2 Student and Faculty Involvement
We now present a few comments on implementation issues including platform, and then briefly address how the project was carried out including the research roles of the students during the project.
2.2.1 Implementation
Our main goal was substantial testing of the various algorithm implementations hoping for empirical results that would both aid in evaluating competing methods and also in future optimization. Other goals included allowing for future implementations of competing or related algorithms, and access to runnable code across the web. With this in mind, we worked toward an extendable, platform-independent, object-oriented implementation. The algorithms were thus implemented in Java with a graphical interface for testing. We chose Java due to its platform independence and its suitability for developing graphical software. Unfortunately, the choice of Java meant that we could not make use of previously existing libraries of geometric algorithms and primitives that have already been developed in C, Pascal, and Smalltalk. However we felt that the tradeoff was worthwhile.
One interesting aspect of the implementation was our experimentation with bucketing. Bucketing, as described earlier, is a technique of dividing the plane into smaller areas, usually of fixed size, called buckets. Geometric objects are then placed in the buckets corresponding to their location on the plane. The description of the "anchored sweep" approach in [BDP97] specifies the size of the buckets to be used. This specification, however, deals only with the asymptotic analysis of the algorithm. Buckets may, in practice, be substantially shrunk, enlarged, or reoriented. For example, it is much simpler to use buckets that are axis aligned (have sides parallel to the x-axis and y-axis). Points can then be placed in the correct bucket by a simple test of the x- and y-coordinates. However, changing the bucket size affects the definition of the "neighborhood" of buckets that needs to be checked. Smaller buckets have the advantage of fewer points per bucket, but the disadvantage of having more buckets to check for each sweep. Our implementation allowed for varying the size of the buckets, so that we could experiment to determine optimal size. We implemented one approach that dynamically chooses a bucket size based on the density of points as well as the size of the polygon.
A web site has been set up to demonstrate our implementations and other undergraduate research projects in computational geometry. The address is
http://www.middlebury.edu/classes/fall97/cx330/.
2.2.2 Research Roles and Interaction
The student work was carried out in a small, dedicated lab, with two desktop machines and network access. The mobile robot was also stored in this room. Of central importance, the lab was in close proximity to the faculty offices. Additionally, the students had access to a larger lab of approximately twenty machines in which they could run their programs at night.
At the start and end of each week, all four participants (faculty and students) met together for one to two hours to discuss current progress and goals for the week. Faculty members would then stop by frequently (usually at least once a day) to check in on progress and answer any questions that might have arisen. The students also frequently visited faculty offices for extended discussions when additional faculty input was required. This plan was maintained throughout the course of the ten-week long summer program. However during the initial two weeks of the summer, the amount of interaction between students and faculty was significantly greater. The first step of the project was simply to read, discuss, and understand the target problems and algorithms. The faculty members initially explained the basic algorithms to the students in a seminar format. Then the students read through the papers on their own, studying the details and asking questions as they arose. The faculty members also discussed implementation details of several fundamental geometric primitives. However, the students, working on their own with each other, did much of the planning of the code including the appropriate use of objects for an object-oriented implementation. They divided the work among themselves according to interest, worked independently in the same room for one or two days, and then periodically merged their work into a single project - especially when basic objects and methods needed revision or refinement. The students also did further independent research into the basic CG literature (especially [BKOS97] and [O'R94]) to investigate implementation issues on the fundamental data structures necessary for the line sweep.
As the project progressed and the student members finished coding the initial algorithms, they were given some flexibility into which extensions and variants they were interested in pursuing. The faculty members also took some part in the coding, which had two benefits. It increased the amount of student-faculty interaction. It also gave the faculty members (by necessity) a closer look at the code, and the opportunity to foresee possible problems that might arise based on student implementation choices.
A final aspect of the summer project was that it took place in the context of a broader summer research program across the sciences. Approximately twenty students took part in the program, distributed across the natural and mathematical sciences including the two students in this project working in computer science, and others working in biology, chemistry, geology, mathematics, physics, and psychology. In addition to several planned social events to encourage interaction among the students, there were also two planned undergraduate research forums. Near the beginning of the summer, several of the faculty members and all of the students gave a brief description of their research areas along with a brief preview of their proposed summer work. At the end of the summer, the students gave a post presentation of their research results. In this way, the students had the opportunity not only to be involved in original research projects, but also were given practice presenting research results in a moderately formal setting.
3. EXPERIMENTAL RESULTS
Several variants of the two algorithms described in the previous section were studied and then implemented by the student members of the research team. In this section we give a sample of some of our experimental results to give a flavor of our work. One of the main purposes of our summer project was to compare the various algorithms for optimal polygon placement in terms of robustness and efficiency. In order to compare them, we wrote standalone Java applications for each algorithm, trying to determine the way the running time is affected by the structure of the input data (i.e., the point set and the polygon to be fit). We ran the applications on several 233MHz Pentium II based Linux machines, all of them with 64Mb of RAM and a cache size of 512K.
Recall that the asymptotic running times of the two algorithms are O(nklog(nm)+m) and O(nklog(mk)+m) where n is the number of input points, m the size of the polygon, and k the number of points contained in the best placement. For testing each of these parameters, we tried to keep the other two constant, so that the results would allow us to analyze them separately.
n: The number of points in the point set should have the greatest impact on the running time. It is easy to vary n and leave m fixed. Unfortunately, the naïve approach of simply increasing the size of the input point set also has the effect of increasing the density of points in the plane, and thus the expected value of k. To compensate, the size of the polygon P can be scaled inversely proportionally to the density of points in order to keep the expected value of k constant.
k: The expected number of points contained can be varied by increasing the area of the polygon or, equivalently, the density of the point set. In order to increase k without changing n, we fix n and change the size of the polygon.
m: Changing m is actually the most difficult. Any change in the number of vertices also changes the shape of the polygon. One approach is simply to create polygons of (approximately) fixed area but with different numbers of vertices, to keep k approximately fixed.
That is, when varying the number of points in the plane for example, we kept the density about the same by increasing the x-y range, so that the optimal placement contains about the same number of points. Comparing the algorithms for the variation of n, we noticed that all of them have similar speeds, except the line sweep implementation, which had a slightly higher rate of growth.
For all the point set sizes, the anchored sweep with dynamic bucketing (which adjusts the size of the buckets to the density of points) is faster even if only slightly. Eventually, for large point sets the higher speed will be more obvious, but certain implementation details (like the speed of the Java code) impose restrictions on how large a point set we can test.
When varying the area, all the algorithms kept the same relation in terms of speed. We found again that the implementations with buckets (both the dynamic and the static one) were faster than the other two. The same held true when we varied the number of vertices of the polygon and kept the area constant.
4. CONCLUSIONS
There are two distinct types of conclusions. The first type of conclusion are those drawn about the actual research project: which algorithm and implementation is superior in which situations and why? The second type of conclusion concerns the concept of student research (especially in computational geometry): what was conducive to successful undergraduate research, and what wasn't? The first question may be of interest only to a limited research audience in CG, while the second is of interest to those in undergraduate computer science education. However, a brief glimpse into the actual results of this undergraduate research project (written by the student participants) will give some insights into what the students learned, and also into how students and faculty both benefited. Thus we will provide a few comments on both issues.
4.1 About Polygon Placement: Conclusions and Further Questions
In theory, the "anchored sweep algorithm" is asymptotically faster by a logarithmic factor when k is large (of the same order as n). However our experimental results indicate that in practice that the standard "line sweep" approach outperforms it. This is most likely attributable to the "bucketing" techniques that were used in the anchored sweep algorithm. Considerable time was spent in this preprocessing phase of initializing the buckets and then bucketing the points, and this extra time was not compensated for by significant speed-up later. This is surprising in that empirical results in other papers have suggested that bucketing usually speeds an algorithm considerably. In our case, however, the bucketing seems to have slowed down the algorithm. This suggests that a next stage in our research will be to develop a better "bucketing" algorithm which will run faster and thus allow us to get experimental results that correctly fit the theoretical run-time analysis of the algorithms. In order to finalize the project, a more in-depth analysis of the line sweep will decide whether the line sweep or the anchored sweep with dynamic buckets will provide the better answer to the optimal polygon placement problem.
There are several questions about these algorithms that still need to be answered. The biggest one is the issue of robustness. Which one of these different approaches to the problem is immune to floating-point round-off errors? How would the running time be affected if we decide to deal properly with all the robustness issues? Another issue is the speed of the Java code. An interpreted language, Java proves to be somewhat slow and still unsuitable for highly computational problems such as the one studied here. Given the wealth of existing CG code libraries in C and Smalltalk, the choice of one of those languages might have been advantageous. However the elegance of the inheritance and the portability of the Java code on the other hand (this summer project was developed using four platforms: MacOS, Win95, AIX, and Linux) seem to balance the impediment of speed when we are looking at non-real-world applications.
Though we did not present the experimental results here, the summer project also explored placement of simple (non-convex) polygons, and placement of polygon annulus regions to contain a maximum number of points. We hope to do similar testing of these algorithms. Another area in which we hope to continue our research is to extend our work to allow rotation as well as translation. This will involve the implementation of some significantly more complex data structures.
4.2 About Undergraduate Research
The undergraduate project had several highlights which contributed greatly to its success. Of greatest importance seems to be a high level of faculty-student interaction. During the implementation and debugging process, there was considerable feedback between students and faculty. The students frequently discussed questions and obstacles with the faculty advisors. As a result of their own experimentation, the students were able to suggest and implement some of their own interesting practical improvements to the algorithms. Though this interaction requires considerable investment on the part of the faculty, it had benefits not only to the enhancement of the educational process but even to the faculty members' research interest.
The interaction of the students researchers in computer science with undergraduate summer research assistants in other areas of the sciences was also beneficial. Students were given the opportunity of presenting their work to a non-specialist audience, and also to get a broader picture of what original research is like.
One of the few goals of the project that was not met during the summer was the testing of the algorithms on "real world" robot localization using data provided by our mobile robot. Though this work remains on a list of future research in which we hope to involve undergraduate students, the difficulties of learning the interface with a new robot proved too great and the aim of downloading the data and testing it in our system too ambitious. In other areas, however, the students far exceeded the goals and expectations we originally had and implemented several additional algorithms. For those initiating such a project for the first time, this does highlight the advantages of involving younger students. The students involved in this project had just finished their sophomore year, and thus have two additional years in which to be involved in a continuing project with the faculty members. With the background these students have now developed, by their senior year it is conceivable that they will be able to tackle substantially more challenging projects.
Throughout our research the students learned much about the field of CG, and many important techniques for implementing algorithms in CG. Among the fundamental techniques of CG studied was the line sweep. Many algorithms in CG can be solved using this line sweep method, and it has become a very useful tool. Students also received valuable experience doing object-oriented programming. Due to the highly pictorial nature of computational geometry, the graphical interface was very helpful. Watching the algorithms working proved for the students to be one of the greatest aids in debugging.
REFERENCES
[BKOS97] M. de Berg, M. van Kreveld, M. Overmars, O. Schwarzkopf, Computational Geometry, (Springer-Verlag, 1997).
[BBDG97] G. Barequet, A. Briggs, M. Dickerson, and M. Goodrich, Offset-Polygon annulus placement problems, LNCS 1272 (Proceedings of the 5th Annual Workshop on Algorithms and Data Structures), 378-391, 1997.
[BDP97] G. Barequet, M. Dickerson, and P. Pau, Translating a convex polygon to contain a maximum number of points, Computational Geometry: Theory and Applications.
[DD98] M. Dickerson and S. Drysdale, The undergraduate algorithms course and recent research in computational geometry, to appear in the Journal of Computing in Small Colleges, Proceedings of the Conference for the Consortium for Computing in Small Colleges, Northeast 1998.
[DS96] M. Dickerson and D. Scharstein, Optimal placement of convex polygons to maximize point containment, Proceedings of the 7th Annual ACM-SIAM Symposium on Discrete Algorithms, 114-121, 1996.
[O'R94] J. O'Rourke, Computational Geometry in C (Cambridge, 1994).
[PS85] F. Preparata and M. Shamos, Computational Geometry: An Introduction (Springer-Verlag, 1985).