Portrait
Philip Claude Caplan
Assistant Professor

about

I am an Assistant Professor of Computer Science at Middlebury College. Before joining Middlebury, I received my PhD and SM in Aeronautics and Astronautics at MIT, working with Bob Haimes and David Darmofal on four-dimensional mesh adaptation. Before that, I studied Mechanical Engineering at McGill University, where I also worked with Siva Nadarajah on aerodynamic shape optimization.

teaching

Term Class
Fall 2021 CSCI 0200: Math Foundations for Computing
Fall 2021 CSCI 0461: Computer Graphics
Spring 2021 CSCI 0145: Introduction to Computing
Winter 2021 CSCI 0461: Computer Graphics
Fall 2020 CSCI 0200: Math Foundations for Computing
Fall 2020 CSCI 0701: Senior Seminar
Spring 2020 CSCI 0200: Math Foundations of Computing
Fall 2019 CSCI 0101: Introduction to Computing
Fall 2019 CSCI 0701: Senior Seminar

research

...

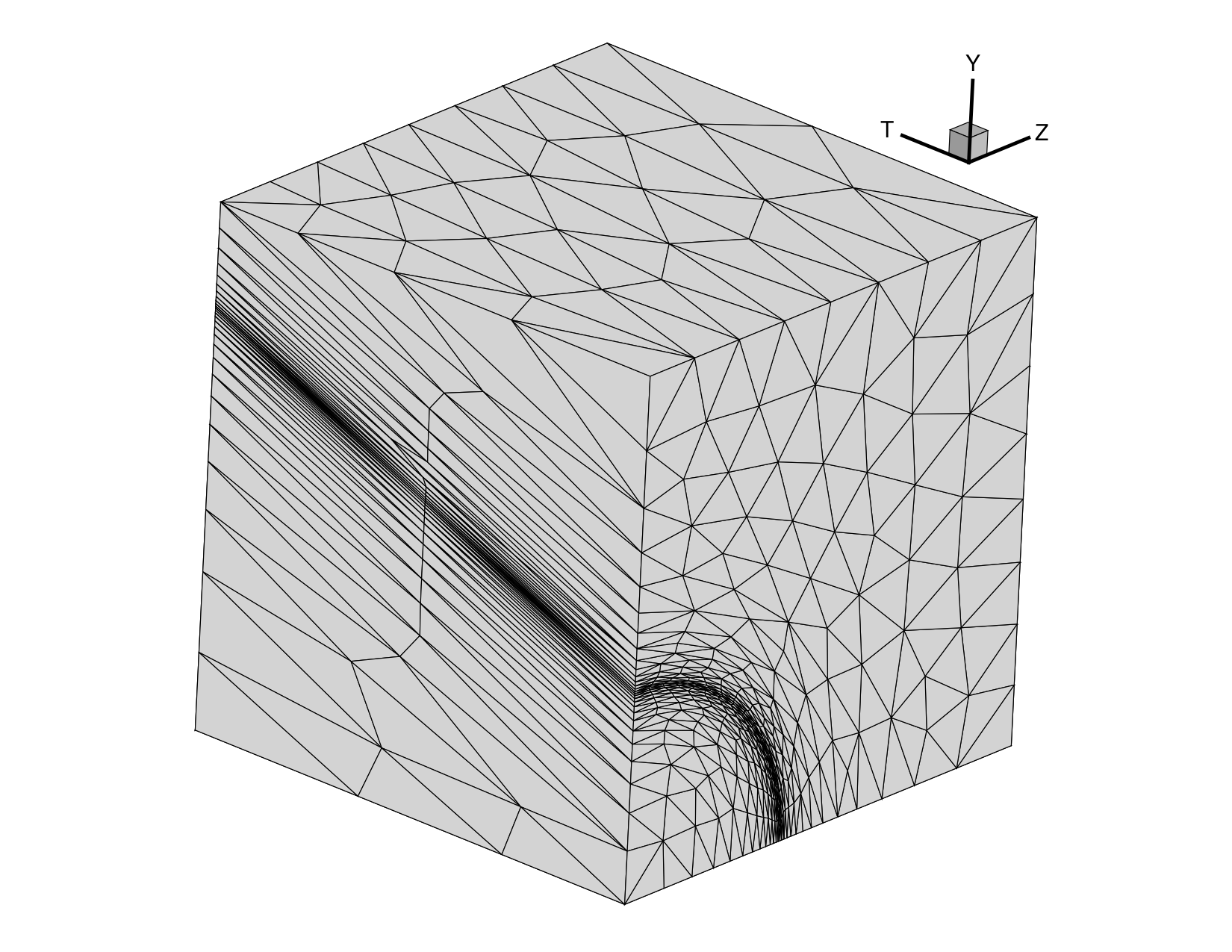
Mesh adaptation

Anisotropic mesh adaptation is important for accurately simulating physical phenomena at reasonable computational costs. This work is driven by the following questions. How can we construct four-dimensional meshes to support time-dependent three-dimensional numerical simulations? How can we adapt meshes about complex geometries? What about time-dependent geometry descriptions? How can we extend some of these techniques to meshes with billions of elements?

... ...

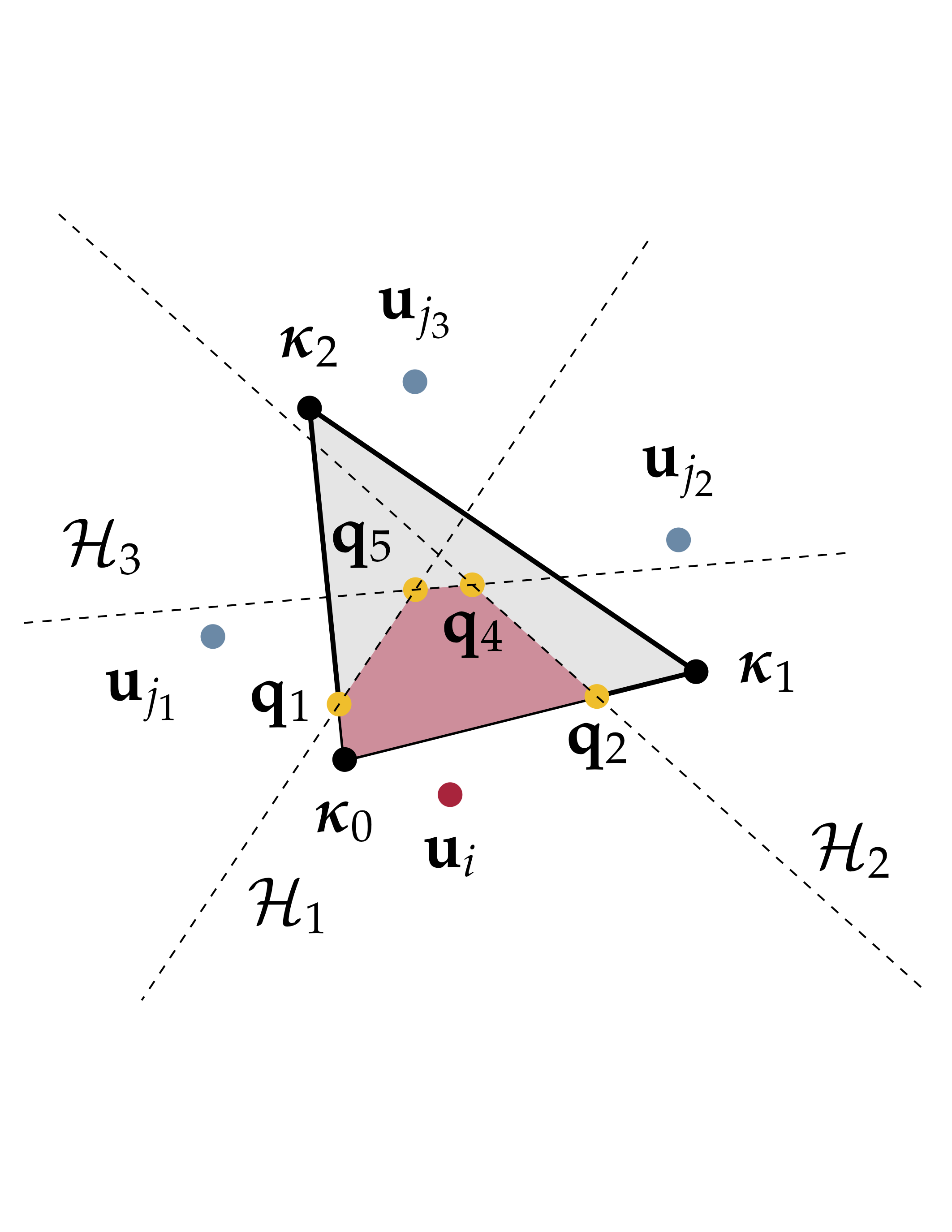
Voronoi diagrams

Ever since my first encounter with Voronoi diagrams, I thought they were beautiful. Then I found out that they naturally appear in nature (giraffe patterns, dragonfly wings, plant leaves, etc.) and I fell even more in love. From a computational geometry standpoint, there are several interesting problems. How do we compute restricted Voronoi diagrams in a dimension-independent manner? How do we construct dimension-independent anisotropic Voronoi diagrams? What if we want the dual Delaunay triangulation to conform to some input geometry description?

...

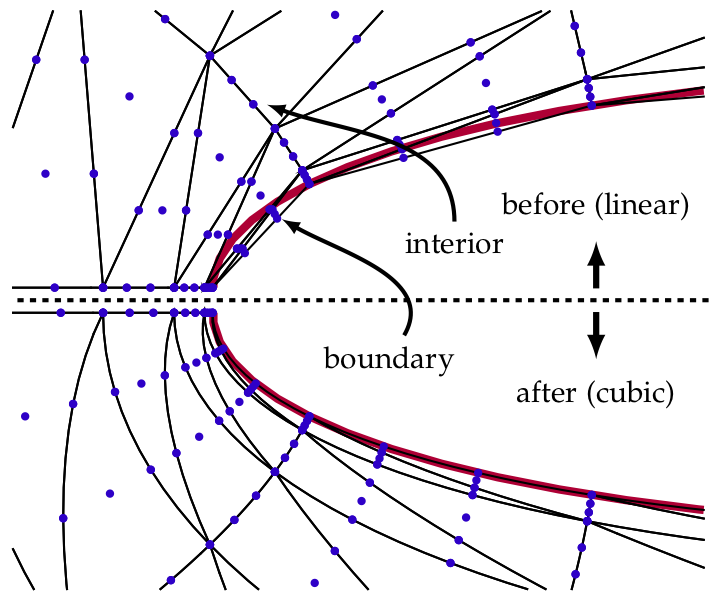
Curvilinear meshing

High-order numerical simulations around complex geometries require a curvilinear description of the mesh. Classical methods for creating these curvilinear meshes consist of computing the location of the interior mesh vertices from the displacement of the boundary ones, such that these boundary vertices lie on the true geometry. However, these methods are not guaranteed to produce a valid mesh, which would halt the simulation! Instead, can we use local mesh operators to produce curvilinear meshes directly and guarantee their validity? How might we visualize curvilinear meshes and high-order solution fields?

For more information about current projects, please visit: go/philipresearch (Middlebury VPN required).

software

  • avro: adaptive Voronoi remesher
    avro is a meshing library that focuses on mesh adaptation, high-order mesh and solution visualization, and the computation of Voronoi diagrams. Most of the algorithms are written in a dimension-independent manner (i.e. the same algorithm is used in 2d, 3d and 4d). I started developing avro in 2017, but rewrote (most of) it when I came to Middlebury in 2019. It's named after the Avro Arrow CF-105, which I think has a really interesting history (it's actually what got me interested in aerospace engineering!).

publications

  • Higher-dimensional power diagrams for semi-discrete optimal transport
    Philip Claude Caplan, Robert Haimes and David L. Darmofal
    International Meshing Roundtable, June 2021.
    @article{Caplan_2020_Four-dimensional_mesh_adaptation,
    author = "Caplan, Philip Claude and Haimes, Robert and Darmofal, David L.",
    title = "Higher-dimensional power diagrams for semi-discrete optimal transport",
    year = "2021",
    month = jun,
    journal = "29th International Meshing Roundtable",
}
  • Four-dimensional anisotropic mesh adaptation
    Philip Claude Caplan, Robert Haimes and David L. Darmofal
    Computer-Aided Design.
    @article{Caplan_2020_Four-dimensional_mesh_adaptation,
    author = "Caplan, Philip Claude and Haimes, Robert, Darmofal, David L. and Marshall C. Galbraith",
    title = "Four-dimensional anisotropic mesh adaptation",
    year = "2020",
    month = nov,
    journal = "Computer-Aided Design",
}
  • Four-dimensional anisotropic mesh adaptation for spacetime numerical simulations
    Philip Claude Caplan
    PhD Thesis, June 2019.
    @phdthesis{Caplan2019_PhdThesis,
    author = "Caplan, Philip Claude",
    title = "Four-dimensional anisotropic mesh adaptation for spacetime numerical simulations",
    year = "2019",
    month = jun,
    school = "Massachusetts Institute of Technology",
    type = {{PhD} Thesis}
}
  • Aerodynamic Design of the Hyperloop Concept
    Max Opgenoord and Philip Claude Caplan
    AIAA Journal, November 2018.
    @article{Caplan_2020_Four-dimensional_mesh_adaptation,
  author = {Opgenoord, Max M. J. and Caplan, Philip C.},
  title = {Aerodynamic Design of the Hyperloop Concept},
  journal = {AIAA Journal},
  volume = {56},
  number = {11},
  pages = {4261-4270},
  year = {2018},
  doi = {10.2514/1.J057103},
  URL = { https://doi.org/10.2514/1.J057103 }
}
  • Isometric embedding of curvilinear meshes defined on Riemannian metric spaces
    Philip Claude Caplan, Robert Haimes, Xevi Roca
    International Meshing Roundtable, September 2018.
    @inproceedings{Caplan_2018_IMR27,
  author = {Caplan, Philip Claude and Haimes, Robert and Roca, Xevi},
  affiliation = {Massachusetts Institute of Technology},
  title = {Isometric Embedding of Curvilinear Meshes Defined on {R}iemannian Metric Spaces},
  booktitle = {Proceedings of the 27th International Meshing Roundtable},
  editor = {},
  publisher = {},
  keyword = {},
  pages = {},
  year = {2018}
}
  • Anisotropic d-simplicial geometry-conforming mesh generation via isometric embeddings
    Philip Claude Caplan, Robert Haimes, David L. Darmofal, Marshall Galbraith
    International Meshing Roundtable, September 2017.
    @inproceedings{Caplan_2017_IMR26,
  author = {Caplan, Philip Claude and Haimes, Robert and Darmofal, David L. and Galbraith, Marshall C.},
  affiliation = {Massachusetts Institute of Technology},
  title = {Anisotropic Geometry-Conforming $d$-simplicial Meshing via Isometric Embeddings},
  note = {26th International Meshing Roundtable},
  journal = {Procedia Engineering},
  editor = {},
  volume = {203},
  publisher = {Springer Berlin Heidelberg},
  keyword = {Engineering},
  pages = {141-153},
  year = {2017}
}